二叉树01：深度优先遍历

1. 概述

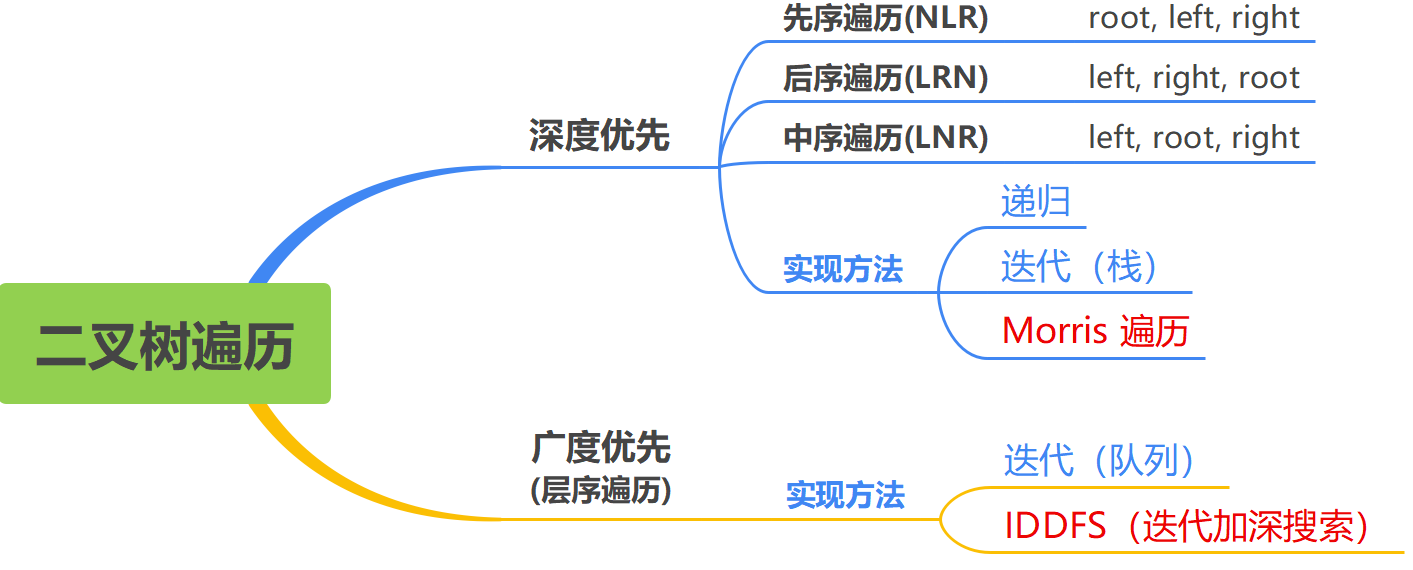
二叉树遍历

图1：二叉树遍历

遍历二叉树，即按照某条搜索路径巡访树中的每个结点，使得每个节点均被访问一次，而且仅被访问一次¹。

深度优先遍历，常见的有递归方式和用栈实现的迭代方式， Morris 遍历虽然空间复杂度很好，但因需在遍历期间改变树结构而不常用。

广度优先遍历，常见的是用队列实现的迭代方式，但需耗费大量内存，而 IDDFS 算法则更节省内存空间。

本文将主要讲述深度优先遍历的递归和迭代的实现方式，其它见后续文章。

代码仓库：https://github.com/patricklaux/perfect-code

2. 递归

先序遍历、中序遍历和后序遍历的过程完全相同，都是从根到左子树再到右子树，差别仅在于何时访问值。

看后面的代码实现，会发现三段递归程序几乎完全相同，仅仅是调整了访问值的次序。

2.1. 先序遍历

先序遍历 (pre-order traversal)：根，左，右

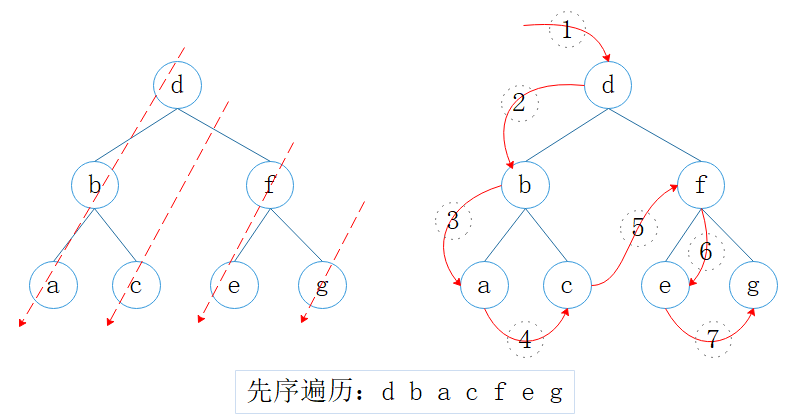
图2：先序遍历

代码实现

private void preorderTraversalR(List<Tuple2<K, V>> kvs, Node<K, V> p) {
    // visit，添加到结果集
    kvs.add(Tuples.of(p.key, p.val));
    if (p.left != null) {
        preorderTraversalR(kvs, p.left);
    }
    if (p.right != null) {
        preorderTraversalR(kvs, p.right);
    }
}

2.2. 中序遍历

中序遍历(in-order traversal)：左，根，右

中序遍历正好是按键的大小排序。

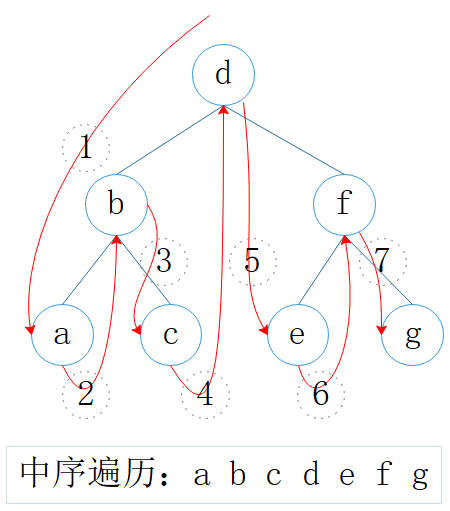
图3：中序遍历

代码实现

private void inorderTraversalR(List<Tuple2<K, V>> kvs, Node<K, V> p) {
    if (p.left != null) {
        inorderTraversalR(kvs, p.left);
    }
    // visit，添加到结果集
    kvs.add(Tuples.of(p.key, p.val));
    if (p.right != null) {
        inorderTraversalR(kvs, p.right);
    }
}

2.3. 后序遍历

后序遍历(postorder traversal)：左，右，根

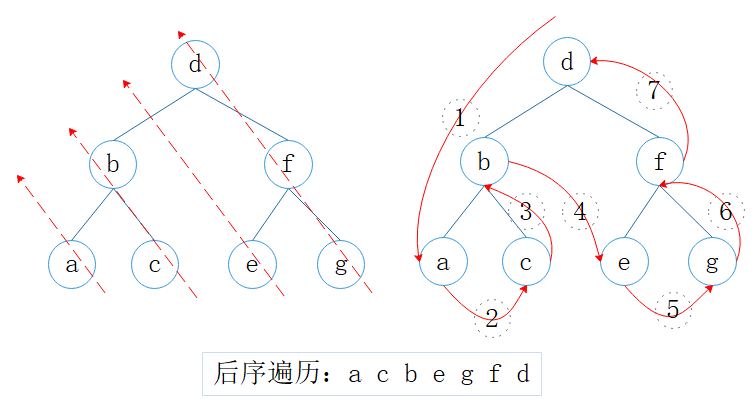
图4：后序遍历

代码实现

private void postorderTraversalR(List<Tuple2<K, V>> kvs, Node<K, V> p) {
    if (p.left != null) {
        postorderTraversalR(kvs, p.left);
    }
    if (p.right != null) {
        postorderTraversalR(kvs, p.right);
    }
    // visit，添加到结果集
    kvs.add(Tuples.of(p.key, p.val));
}

3. 迭代

递归其实是隐式用栈；而迭代则是显式用栈。

3.1. 先序遍历

先序遍历的逻辑比较简单。

压入根节点；
弹出栈顶节点，访问值；
栈后进先出，所以右孩子先入栈，左孩子后入栈；
重复2~3，直到栈为空。

public void preorderTraversal(List<Tuple2<K, V>> kvs) {
    if (root == null) {
        return;
    }
    Stack<Node<K, V>> stack = new Stack<>();
    stack.push(root);
    while (!stack.isEmpty()) {
        Node<K, V> p = stack.pop();
        kvs.add(Tuples.of(p.key, p.val));
        if (p.right != null) {
            stack.push(p.right);
        }
        if (p.left != null) {
            stack.push(p.left);
        }
    }
}

3.2. 中序遍历

中序遍历的逻辑稍稍复杂。

根节点入栈；
左子树全部入栈；
弹出栈顶节点，访问值；
当前节点是否有右孩子：有，跳转2，右孩子的左子树入栈；无，因为左孩子为空或已访问值，跳转3访问上层节点。
重复2~4，直到栈为空。

核心思路：

先将根节点及左子树全部入栈，然后向上移动：弹出栈顶节点，访问该节点，中序遍历该节点的右子树；弹出栈顶节点，访问该节点，中序遍历该节点右子树……

public void inorderTraversal(List<Tuple2<K, V>> kvs) {
    if (root == null) {
        return;
    }
    Stack<Node<K, V>> stack = new Stack<>();
    Node<K, V> p = root;
    while (p != null || !stack.isEmpty()) {
        if (p != null) {
            stack.push(p);
            p = p.left;
        } else {
            p = stack.pop();
            kvs.add(Tuples.of(p.key, p.val));
            p = p.right;
        }
    }
}

3.3. 后序遍历

后序遍历的逻辑最为复杂。

核心思路：

先将根节点及左子树全部入栈，然后向上移动：弹出栈顶节点，后序遍历该节点右子树，访问该节点；弹出栈顶节点，后序遍历该节点右子树，访问该节点……

复杂主要是因为要后序遍历完当前节点的右子树，然后再访问当前节点。

所以，一个节点第一次出栈，如果其有右子树，则需将该节点重新入栈，先后序遍历右子树；第二次出栈时，再访问当前节点并向上移动。

但是，怎么才能知道一个节点是第一次出栈还是第二次出栈呢？

这时，需要增加一个变量 prev 来与当前节点的右孩子进行比较：

如果 prev 与当前节点的右孩子非同一节点，则为第一次弹出，遍历右子树；

如果 prev 与当前节点的右孩子是同一节点，则为第二次弹出，访问当前节点并向上层移动。

例：当前节点是 b，由于要先访问 c，所以先将 b 再次入栈，然后访问 c 并设 prev = c；第二次弹出 b 时，b 的右孩子等于 prev，访问 b 并向上移动。

public void postorderTraversal(List<Tuple2<K, V>> kvs) {
    if (root == null) {
        return;
    }
    Stack<Node<K, V>> stack = new Stack<>();
    Node<K, V> p = root, prev = null;
    while (p != null || !stack.empty()) {
        if (p != null) {
            stack.push(p);
            p = p.left;
        } else {
            // 可以改成 peek()，避免重新入栈
            p = stack.pop();
            if (p.right != null && p.right != prev) {
                stack.push(p);
                p = p.right;
            } else {
                kvs.add(Tuples.of(p.key, p.val));
                // 如果 p 为某个节点的右孩子，那么访问完 p 的下一循环出栈的一定是 p 的父节点
                prev = p;
                p = null;
            }
        }
    }
}

3.4. 后序遍历的另一种实现

给每个节点一个状态，用该状态判断其是否已遍历右子树。

这个的代码逻辑相当直观，具体代码如下：

public void postorderTraversal1(List<Tuple2<K, V>> kvs) {
    if (root == null) {
        return;
    }
    Stack<Tuple2<Node<K, V>, Integer>> stack = new Stack<>();
    // 1.根节点入栈，初始状态为 0
    stack.push(Tuples.of(root, 0));
    while (!stack.isEmpty()) {
        // 2.弹出栈顶元素
        Tuple2<Node<K, V>, Integer> tuple = stack.pop();
        // 3.判断状态
        Node<K, V> p = tuple.getT1();
        if (tuple.getT2() == 1) {
            // 3.1. 如果状态为 1，表示已经遍历右子树，添加键值到结果集（访问节点）
            kvs.add(Tuples.of(p.key, p.val));
        } else {
            // 3.1. 如果状态为 0，表示还未遍历右子树，修改状态为1，并重新入栈
            stack.push(tuple.mapT2(t2 -> 1));
            if (p.right != null) {
                // 3.2.右孩子先入栈
                stack.push(Tuples.of(p.right, 0));
            }
            if (p.left != null) {
                // 3.3.左孩子后入栈
                stack.push(Tuples.of(p.left, 0));
            }
        }
    }
}

4. 小结

迭代方式的逻辑稍微有点绕，但其实理解之后并不复杂。

空间复杂度：栈深最大为树的高度，所以是 \( O(h) \)。

时间复杂度：仅跟节点数 n 相关，所以是 \( O(n) \)。虽然后序遍历需两次入栈(三次经过同一节点)，但依然是常数时间，所以也是\( O(n) \)。

参考资料

严蔚敏, 吴伟民. 数据结构(C语言版)[M]. 清华大学出版社, 2007. ↩︎

1. 概述#

2. 递归#

2.1. 先序遍历#

2.2. 中序遍历#

2.3. 后序遍历#

3. 迭代#

3.1. 先序遍历#

3.2. 中序遍历#

3.3. 后序遍历#

3.4. 后序遍历的另一种实现#

4. 小结#

参考资料#

1. 概述

2. 递归

2.1. 先序遍历

2.2. 中序遍历

2.3. 后序遍历

3. 迭代

3.1. 先序遍历

3.2. 中序遍历

3.3. 后序遍历

3.4. 后序遍历的另一种实现

4. 小结

参考资料