1. 概述

前一篇文章介绍了深度优先遍历的递归实现和迭代实现，这两种方式的时间复杂度都是 \( O(n) \)，空间复杂度都是 \( O(h) \)，本文将要介绍的 Morris 遍历的时间复杂度依然为 \( O(n) \)，但空间复杂度仅为 \( O(1) \)，其中 n 为节点数，h 为树的高度。

算法来历

1968年，《计算机程序设计艺术》的作者 Knuth 提出了一个问题：设计一个无需堆栈和额外标志域的非递归的中序遍历算法，且当遍历结束时树结构不变。此后，诞生了许多解决方案，而Morris 遍历是其中最优雅的一种（见参考资料1）1。

此算法由 Joseph M. MORRIS 在1979年的论文 “Traversing Binary Trees Simply and Cheaply2” 中首次提出。顺便再说一句，这个 MORRIS 正是大名鼎鼎的 KMP 算法的作者之一。

代码仓库：https://github.com/patricklaux/perfect-code

2. 算法解析

线索二叉树

如果了解线索二叉树的话，肯定对前驱和后继非常熟悉。

通过在二叉树节点增加前驱和后继指针，可以非常方便地进行向前查找、向后查找和遍历等线性化操作，相当于是二叉树和链表的结合。这其中指向前驱和后继的指针称之为线索，而包含线索的二叉树则称之为线索二叉树(Threaded Binary Tree)3。

譬如 Java 的 HashMap 中的 红黑树节点，就增加了 prev 和 next 指针，其节点结构类似如下：

class TreeNode<K,V> {
    TreeNode<K,V> parent;	// 父节点
    TreeNode<K,V> left;		// 左孩子
    TreeNode<K,V> right;	// 右孩子
    TreeNode<K,V> prev;		// 前驱
    TreeNode<K,V> next;		// 后继
    boolean red;			// 颜色
}

这种方式需要额外内存来保存前驱和后继指针，那么是不是有一些其它方式来避免这个问题呢？

对于二叉树，如果 n 为节点数，那么会有 2n 个链接，其中有 n+1 个空链接。那么，一个朴素的想法是使用节点的空链接来保存前驱和后继。

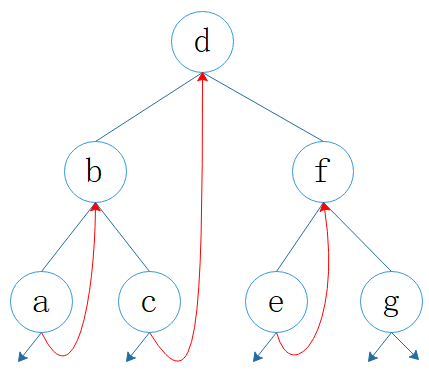
图1：线索二叉树

图1：线索二叉树

如上图所示，利用空的右孩子指针指向其后继节点（红色线），然后就可以用 node.right 来遍历了。

特别注意：Morris 遍历算法的后继指针是在遍历过程中动态建立和删除的。

另外，能够利用空的右孩子来保存后继指针，这其实隐含了一个假设：

如果一棵二叉查找树中的一个节点有两个孩子（非空，如 d, b, f），那么它的前驱没有右孩子，它的后继没有左孩子。

好吧，这其实是《算法导论》中的一道证明题，根据二叉查找树左小右大的基本性质，即可证明此假设成立，证明过程就不展开了。

3. 算法实现

既然高老爷子的问题是关于中序遍历的，那么就先从中序遍历开始吧。

3.1. 中序遍历

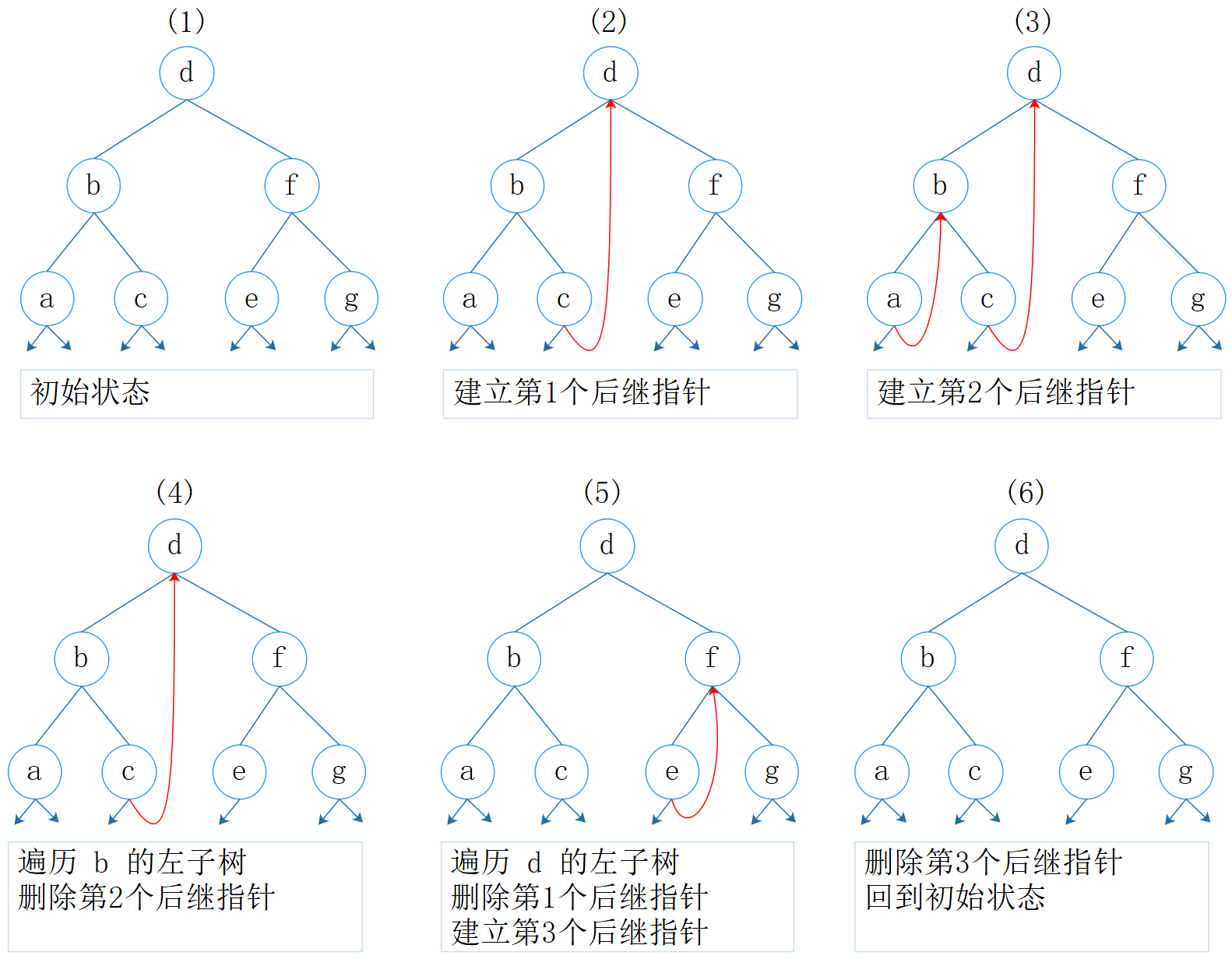
图2：Morris中序遍历过程

图2：Morris 中序遍历过程

过程描述：

  1. 初始状态；
  2. 当前节点为 d，d 有左孩子，找到 d 的前驱节点 c，c 的右指针指向 d；
  3. d 有左孩子，向左走，当前节点为 b，找到 b 的前驱节点 a，a 的右指针指向 b；
  4. b 有左孩子，向左走，当前节点为 a，a 没有前驱节点，访问 a；通过 a 的右指针找到后继节点 b，当前节点为b，访问 b，删除前驱指针；通过 b 的右指针找到 c，当前节点为c， 访问 c；通过 c 的右指针找到 d，当前节点为 d，访问 d;
  5. 通过 d 的右指针找到 f, f 有左孩子，找到 f 的前驱节点 e，e 的前驱节点指向 f；
  6. f 有左孩子，向左走，当前节点为 e，访问 e；通过 e 的右指针找到后继节点 f，当前节点为f，访问 f，删除前驱指针；通过 f 的右指针找到 g，当前节点为 g，访问 g；g 的右指针指向空，遍历结束，回到初始状态。

核心思路：

  1. 是否有左孩子：有，查找当前节点的前驱，并将前驱节点的右指针指向当前节点，向左走；无，向右走；
  2. 重复 1，直到当前节点的左孩子为空；
  3. 访问当前节点，判断左子树是否已遍历：是，删除前驱指针，转到右指针指向的节点；否：回到 过程 1；
  4. 重复 3，直到右指针指向的节点为空则结束遍历。

代码实现：

public void morrisInorderTraversal(List<Tuple2<K, V>> kvs) {
    Node<K, V> p = root, pred;
    while (p != null) {
        // 1. 判断左孩子是否为空
        // 1.1. 左孩子不为空，需先遍历左子树
        if (p.left != null) {
            // 2.查找前驱节点
            pred = p.left;
            while (pred.right != null && pred.right != p) {
                pred = pred.right;
            }
            // 3.判断前驱节点的右孩子是否为空
            // 3.1. 前驱节点的右孩子为空，表示第一次经过该节点（还未遍历左子树）
            if (pred.right == null) {
                pred.right = p;	//右孩子指针指向后继节点
                p = p.left;
            } else {
                // 3.2. 前驱节点的右孩子不为空，表示第二次经过该节点（已经遍历左子树）
                kvs.add(Tuples.of(p.key, p.val));
                pred.right = null;	//去除指向后继节点的指针
                p = p.right;
            }
        } else {
            // 1.2. 左孩子为空，无需遍历左子树，访问当前节点的值
            kvs.add(Tuples.of(p.key, p.val));
            p = p.right;
        }
    }
}

3.2. 先序遍历

先序遍历的代码几乎与中序遍历完全一致，区别仅在于何时访问值。

public void morrisPreorderTraversal(List<Tuple2<K, V>> kvs) {
    Node<K, V> p = root, pred;
    while (p != null) {
        if (p.left != null) {
            pred = p.left;
            while (pred.right != null && pred.right != p) {
                pred = pred.right;
            }
            if (pred.right == null) {
                kvs.add(Tuples.of(p.key, p.val));
                pred.right = p;
                p = p.left;
            } else {
                pred.right = null;
                p = p.right;
            }
        } else {
            kvs.add(Tuples.of(p.key, p.val));
            p = p.right;
        }
    }
}

3.3. 后序遍历

后序遍历还是最复杂的。

后序遍历

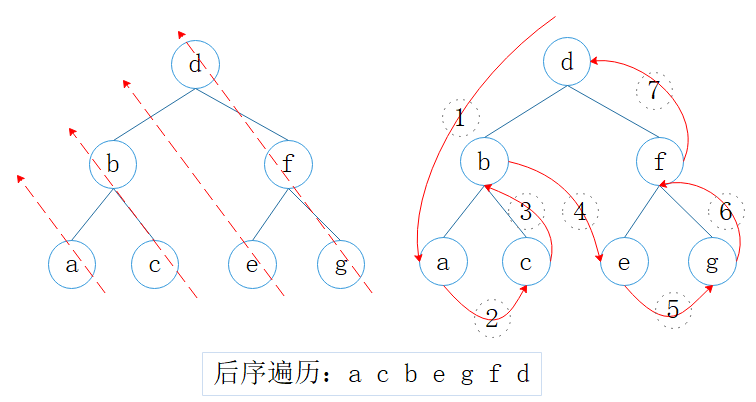
图3：后序遍历

如前文所述，后序遍历需要先访问右子树，再访问当前节点。但由于Morris遍历没有栈，所以无法通过再次入栈来调换访问顺序。

我们再观察下上面的左图，会发现只要将节点反转后访问即是后序遍历。

  1. a 反转后还是a，访问 a；
  2. b, c 反转后是 c, b，依次访问 c, b；
  3. e 反转后还是 e，访问 e；
  4. d, f, g 反转后是 g, f, d，依次访问 g, f, d。

结束，正好是：a, c, b, e, g, f, d。

public void morrisPostorderTraversal(List<Tuple2<K, V>> kvs) {
    Node<K, V> p = root, pred;
    while (p != null) {
        if (p.left != null) {
            pred = p.left;
            while (pred.right != null && pred.right != p) {
                pred = pred.right;
            }
            if (pred.right == null) {
                pred.right = p;
                p = p.left;
            } else {
                pred.right = null;
                // 反转并访问值
                reverseAdd(kvs, p.left);
                p = p.right;
            }
        } else {
            p = p.right;
        }
    }
    // 反转并访问值
    reverseAdd(kvs, root);
}

private void reverseAdd(List<Tuple2<K, V>> kvs, Node<K, V> node) {
    // 反转
    Node<K, V> tail = reverse(node);
    Node<K, V> next = tail;
    while (next != null) {
        kvs.add(Tuples.of(next.key, next.val));
        next = next.right;
    }
    // 还原
    reverse(tail);
}

private Node<K, V> reverse(Node<K, V> node) {
    Node<K, V> prev = null, next;
    while (node != null) {
        next = node.right;
        node.right = prev;
        prev = node;
        node = next;
    }
    return prev;
}

Morris 遍历在原论文中仅有中序遍历，推广到先序遍历还不错，但推广到后序遍历就没那么优雅了。

4. 小结

Morris 遍历是优点和缺点都非常明显的一个算法。

优点：无需使用额外的栈空间，空间复杂度为 \( O(1) \)。

缺点：遍历过程中改变了树结构，一次遍历完成之前不能开始另一次遍历。

另，参考资料 11 证明了 Morris 遍历其实与递归遍历一样，同样隐式使用了栈（如图2 所示的红色线条），这个栈最大时等于树高（如图2 所示最多时会有 2 条红色线），因此其与显式使用栈的遍历是可以等价转换的。

Morris 遍历虽然是隐式用栈，但并没使用额外的栈空间，所以其空间复杂度依然是 \( O(1) \)。

参考资料

  1. MATETI, MANGHIRMALANI. MORRIS TREE TRAVERSAL ALGORITHM RECONSIDERED[J]. SCI COMPUT PROGRAM, 1988. ↩︎ ↩︎

  2. Morris J M . Traversing Binary Trees Simply and Cheaply[J]. Information Processing Letters, 1979, 9(5):197-200. ↩︎

  3. 严蔚敏, 吴伟民. 数据结构(C语言版)[M]. 清华大学出版社, 2007. ↩︎