1. 概述
IDDFS (Iterative deepening depth-first search):迭代加深搜索,是一种状态空间/图的搜索策略。
其空间复杂度仅为 \( O(d) \),相比用队列实现层序遍历所需的 \( O(b^d) \) 空间复杂度,极大地节约了空间开销,b 为分支因子,d 为深度。
从三个维度来分析,空间开销、时间性能和求解路径的代价,IDDFS 都接近最优,是一个非常优秀的算法。
本文主要介绍用 IDDFS 算法实现二叉树的层序遍历,如对其它方面的搜索运用感兴趣,可阅读参考资料1。
代码仓库:https://github.com/patricklaux/perfect-code
2. 使用队列实现层序遍历
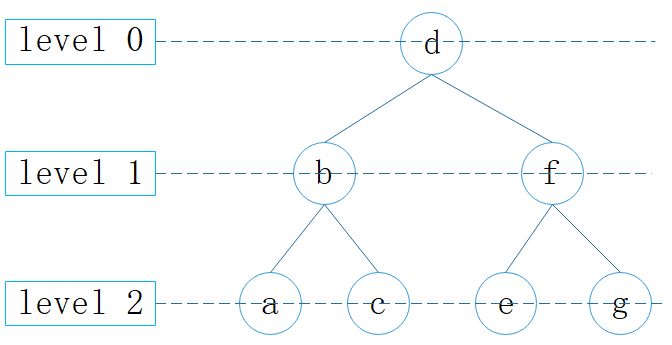
层序遍历:即为按层顺序访问,所有深度为 d 的节点在深度为 d+1 的节点之前访问——(d, b, f, a, c, e, g)。
使用队列实现层序遍历并不复杂,代码如下:
public void levelOrderTraversal(List<Tuple2<K, V>> kvs) {
if (root == null) {
return;
}
ArrayDeque<Node<K, V>> queue = new ArrayDeque<>(size.get() / 2);
queue.push(root);
while (!queue.isEmpty()) {
Node<K, V> p = queue.poll();
kvs.add(Tuples.of(p.key, p.val));
if (p.left != null) {
queue.offer(p.left);
}
if (p.right != null) {
queue.offer(p.right);
}
}
}
常见的算法书在介绍层序遍历时都采用队列来实现,这种算法被称为标准 BFS。
遍历每层都需先将整层节点全部入队,然后再出队,因此其空间复杂度为 \( O(b^d) \),b 为分支因子,d 为深度。
每个节点仅需入队出队 1 次,因此时间复杂度为 \( O(n) \),n 为节点数。如果用深度来表示,同样是 \( O(b^d) \)。
3. IDDFS
迭代加深搜索,顾名思义,即每次搜索一层,如果指定层无目标解,则继续搜索下一层。
如此循环迭代,直到找到目标解或已遍历完所有节点为止。
文字描述远没有代码直观,还是直接看伪代码:
iddfs() {
// 每次循环深度+1
for (depth = 0; ; ++depth) {
// 搜索指定层
Tuple2<Boolean, Node> tuple2 = dls(depth);
// 如果指定层已无节点(表示已遍历完所有节点),退出循环
if (tuple2.getT1 == false) break;
// 如果已找到目标解,退出循环
if (tuple2.getT2 is goal) break;
}
}
// 搜索指定层,返回二元组:1.指定层是否有节点;2.目标解
Tuple2<Boolean, Node> dls(depth);
3.1. IDDFS 之递归层序遍历
IDDFS 主要用于查找目标解,而这里将 IDDFS 用于层序遍历,需做一个小改动:查找目标解改为遍历指定层。
public void iddfsR(List<Tuple2<K, V>> kvs) {
if (root == null) {
return;
}
int depth = 0;
while (dlsR(kvs, root, depth)) {
++depth;
}
}
// 遍历指定层
private boolean dlsR(List<Tuple2<K, V>> kvs, Node<K, V> node, int depth) {
// 1.是否到达指定层
if (depth == 0) {
// 1.1.depth为0,到达指定层,访问节点
kvs.add(Tuples.of(node.key, node.val));
// 指定层存在,总是返回 true
return true;
} else {
// 1.2 depth>0,未到指定层,继续递归
// 指定层是否存在(左子树或右子树存在指定层即返回 true)
boolean remaining = false;
// 2.1. 左子树继续递归(每次进入下一层,depth-1)
if (null != node.left && dls(kvs, node.left, depth - 1)) {
remaining = true;
}
// 2.2. 右子树继续递归(每次进入下一层,depth-1)
if (null != node.right && dls(kvs, node.right, depth - 1)) {
remaining = true;
}
// 返回指定层是否存在
return remaining;
}
}
3.2. IDDFS 之非递归层序遍历
public void iddfs(List<Tuple2<K, V>> kvs) {
if (root == null) {
return;
}
int depth = 0;
while (iddfs(kvs, depth)) {
++depth;
}
}
private boolean dls(List<Tuple2<K, V>> kvs, int depth) {
// 使用数组记录当前的分支路径
Node<K, V>[] path = new Node[depth + 1];
// 当前所在的层
int curDep = 0;
path[0] = root;
boolean remaining = false;
while (curDep >= 0) {
Node<K, V> p = path[curDep];
if (curDep < depth) {
// 获取下层节点,用于判断是否已经遍历
Node<K, V> ch = path[curDep + 1];
// 先遍历左子树
if (p.left != null && p.left != ch) {
if (p.right != ch) {
path[++curDep] = p.left;
continue;
}
}
// 后遍历右子树
if (p.right != null && p.right != ch) {
path[++curDep] = p.right;
continue;
}
} else {
remaining = true;
kvs.add(Tuples.of(p.key, p.val));
}
// 已遍历左右子树(或无左右子树),回退到上层节点
--curDep;
}
return remaining;
}
非递归实现多了一个数组 path 来记录当前的分支路径,还有一个数值 curDep 来控制进入下一层还是回退上一层。
这其实是用数组来模拟栈(可以直接用栈来实现,但代码反而会更复杂一些)。
PS: 之前写字典树需用到层序遍历,怕内存爆炸不敢用队列,翻了几本算法书,又在网上溜达了一圈,也没找到一个合适的算法。 于是,闭门造车了差不多一周,自己实现了一个无需队列的非递归的层序遍历,当时还以为自己发现了个新算法,激动了半天。 激动过后又觉得不太可能,于是继续查资料,才发现原来我写的其实是 IDDFS 的非递归实现。 虽然如此,但依然觉得这个非递归实现很美,借用知乎问题《被自己写的代码美哭是一种什么样的体验?》,哎,都要被自己的代码给美哭了。
3.3. 分析
空间复杂度
IDDFS 仅需存储当前正在访问的分支路径,因此空间复杂度为 \( O(d) \)。
时间复杂度
IDDFS 的时间复杂度与标准BFS 相同,即 \( O(b^d) \),详细证明见参考资料1。
这个结论似乎有点反直觉,从代码来看 IDDFS 的时间开销肯定比用队列实现的标准 BFS 要大:遍历 d 层时:d-1 层共需展开 2 次,d-2 层共需展开 3 次 …… 0 层共需要展 d+1 次。
我们试计算下完美二叉树当 d=4 时所需的时间开销:
$$\sum_{d=0}^4(4+1-d)2^d=5+8+12+16+16=57$$57 小于节点数 31 的 2 倍,虽然会稍慢一些,但时间复杂度依然为 \( O(b^d) \)。
这主要是因为越靠近底层,节点数越多,对于完美二叉树,当前层的节点数比其所有上层节点数之和多 1。
对于非二叉树,分支因子 b 越大,IDDFS 就会越接近于标准BFS 的时间开销,有兴趣可以试计算一下。
小结
IDDFS 具有与 DFS 相同的空间开销,并接近于标准 BFS 的时间效率。
IDDFS 可以很好地与其它算法相结合,有非常广泛的应用,希望更多了解可阅读参考资料1。