时隔多年又重新实现了一遍 AVL树,并且进行了深度优化,所以有些心得。
首先,我会介绍6种失衡类型和4种旋转;
然后,重点描述插入和删除的优化实现,并将给出严谨的分析和证明,解释为什么可以这么优化;
最后,我会用 AVL 树与 Java 的 TreeMap (红黑树)进行性能对比,以验证优化结果。
代码仓库:https://github.com/patricklaux/perfect-code
1. 简介
AVL 树是一种自平衡二叉查找树(Self-balancing binary search tree),得名于其两位作者的首字母1: Georgy Adelson-Velsky 和 Evgenii Landis。
相比于二叉查找树最坏情况下时间复杂度为 \( O(n) \),AVL树查找、插入和删除的平均时间复杂度和最坏时间复杂度均为 \( O(log_2n) \),其中 n 为树的节点数。
2. 高度与平衡因子
AVL树的平衡性质:其任意节点的左子树和右子树的高度差的绝对值小于等于1。
2.1. AVL节点
private class AvlNode<K, V> {
K key; // 键
V val; // 值
byte height; // 高度
AvlNode<K, V> left; // 左孩子
AvlNode<K, V> right; //右孩子
}
2.2. 获取高度
// 空树的高度定义为 -1。
private byte height(AvlNode<K, V> node) {
return (node == null) ? -1 : node.height;
}
2.3. 更新高度
// 取左右子树的高度的大者再加1,即为父节点的高度
private void updateHeight(AvlNode<K, V> parent) {
parent.height = (byte) (Math.max(height(parent.left), height(parent.right)) + 1);
}
2.4. 平衡因子
二叉查找树的平衡因子 BF (Balance Factor) 的定义为两棵子树的高度之差。
// 平衡因子的计算
private int balanceFactor(AvlNode<K, V> parent) {
return height(parent.left) - height(parent.right);
}
根据AVL树的性质,其任意节点的平衡因子只能为 1,0 和 -1。当一个节点的平衡因子大于 1 或小于 -1,我们可以通过旋转来恢复其平衡性质。
3. 失衡和旋转
AVL树的失衡可以总结为6种类型:LL,L,RR,R,LR,RL。
3.1. 单旋转
3.1.1. LL(右旋)
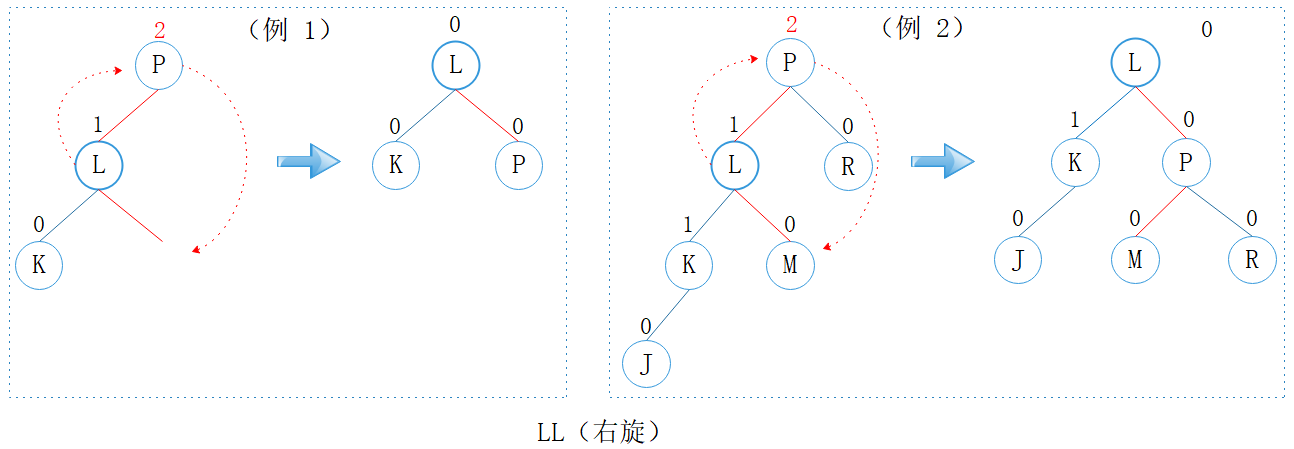
图1: LL型
观察上图的两个小例子,我们可以发现 P 节点的平衡因子为 2,其左孩子 L 的平衡因子为 1,都是左子树更重(left-heavy),因此称为 LL。
其中 P 节点的平衡因子大于 1,因此需要修正。
对于 LL 型,只需一次右旋即可恢复平衡性质。
private Node<K, V> rotateLeft(Node<K, V> parent) {
Node<K, V> right = parent.right;
parent.right = right.left;
right.left = parent;
updateHeight(parent);
updateHeight(right);
return right;
}
3.1.2. L(右旋)
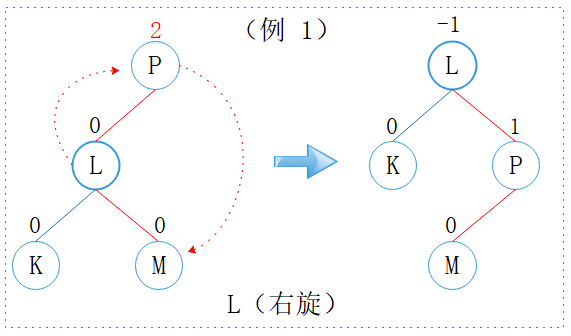
图2: L型
观察上图,我们可以发现 P 节点的平衡因子为 2,左子树更重;其左孩子 L 的平衡因子为 0,因此称为 L。
L 型与 LL 型一样,只需一次右旋即可恢复平衡性质。
但不一样的是:L 型旋转之后该子树的高度不变。
L 型只有在删除节点时才会出现。 为什么? 二叉查找树总是将新节点添加为叶子节点,且一次只能增加一个节点。 如图2所示,当P节点无右子树时,先添加任意一个叶子节点(K 或 M)都会触发旋转,L 节点不可能同时有两个孩子。 因此,这种情形只有在删除 P 节点的右孩子才会出现。
3.1.3. RR(左旋)
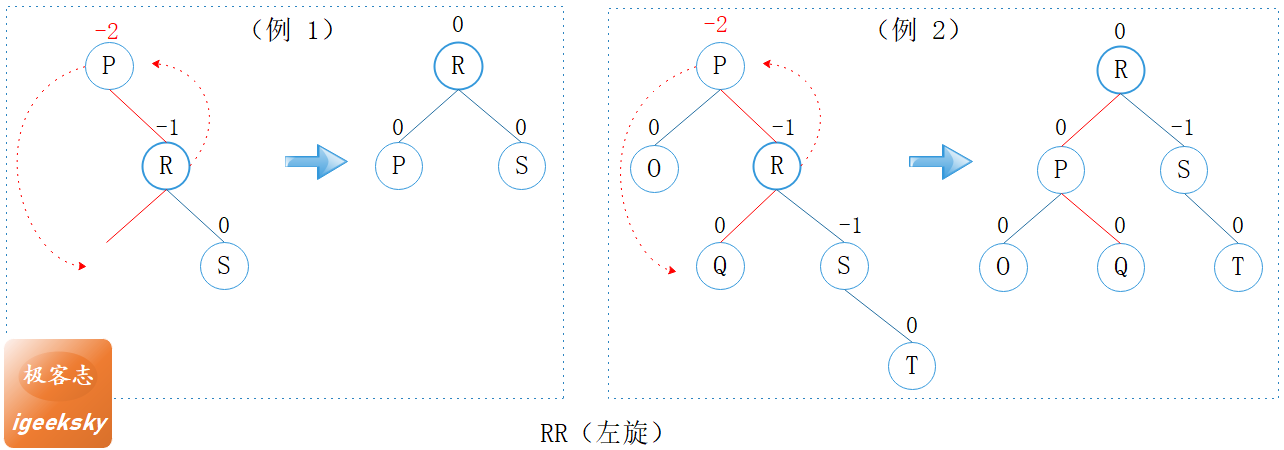
图3: RR型
观察上图的两个小例子,我们可以发现 P 节点的平衡因子为 -2,其右孩子 R 的平衡因子为 -1,都是右子树更重(right-heavy),因此称为 RR。
其中 P 节点的平衡因子小于 -1,因此需要修正。
对于RR型,只需一次左旋即可恢复平衡性质。
private Node<K, V> rotateRight(Node<K, V> parent) {
Node<K, V> left = parent.left;
parent.left = left.right;
left.right = parent;
updateHeight(parent);
updateHeight(left);
return left;
}
3.1.4. R(左旋)
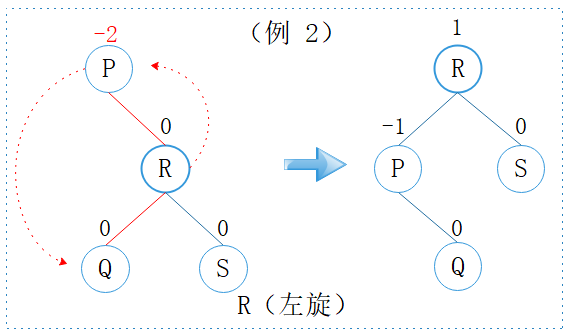
图4: R型
观察上图,我们可以发现 P 节点的平衡因子为 -2,右子树更重;其右孩子 R 的平衡因子为 0,因此称为 R。
R 型与 RR 型一样,只需一次左旋即可恢复平衡性质。
但不一样的是:R型旋转之后该子树的高度不变。
R 型只有在删除节点时才会出现。
3.2. 双旋转
3.2.1. LR(先左旋后右旋)
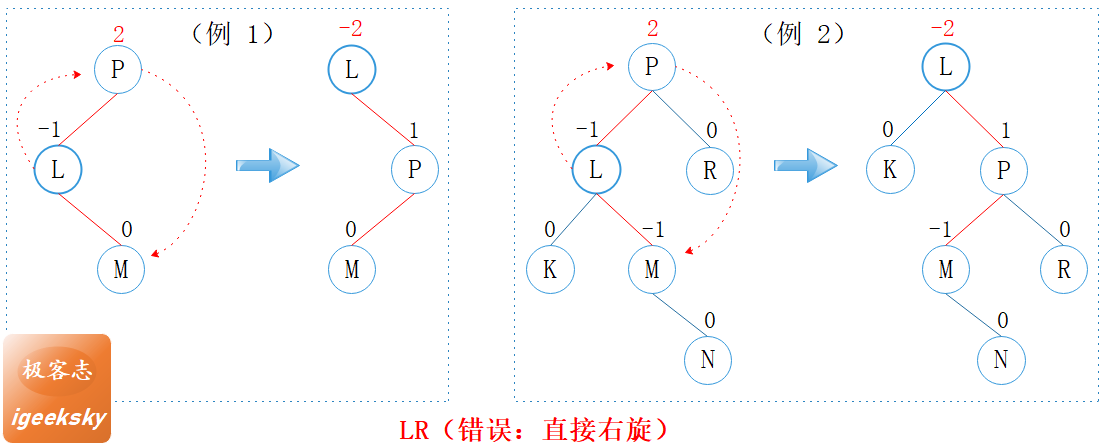
图5: LR型错误示例
观察上图的两个小例子,我们可以发现 P 节点的平衡因子为 2,左子树更重;其左孩子 L 的平衡因子为 -1,右子树更重,因此称为 LR。
其中 P 节点的平衡因子大于 1,因此需要修正。
对于 LR 型,如上图所示,直接右旋无法恢复平衡性质。
正确的做法应该是如下图所示,先左旋后右旋。
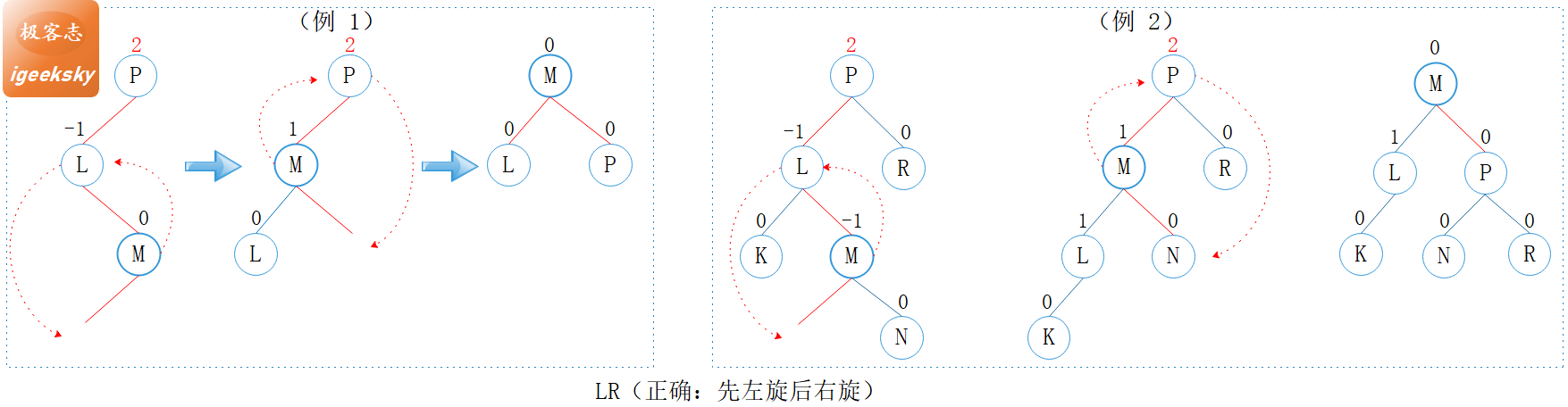
图6: LR型正确示例
private Node<K, V> rotateLeftRight(Node<K, V> parent) {
parent.left = rotateLeft(parent.left);
return rotateRight(parent);
}
3.2.2. RL(先右旋后左旋)
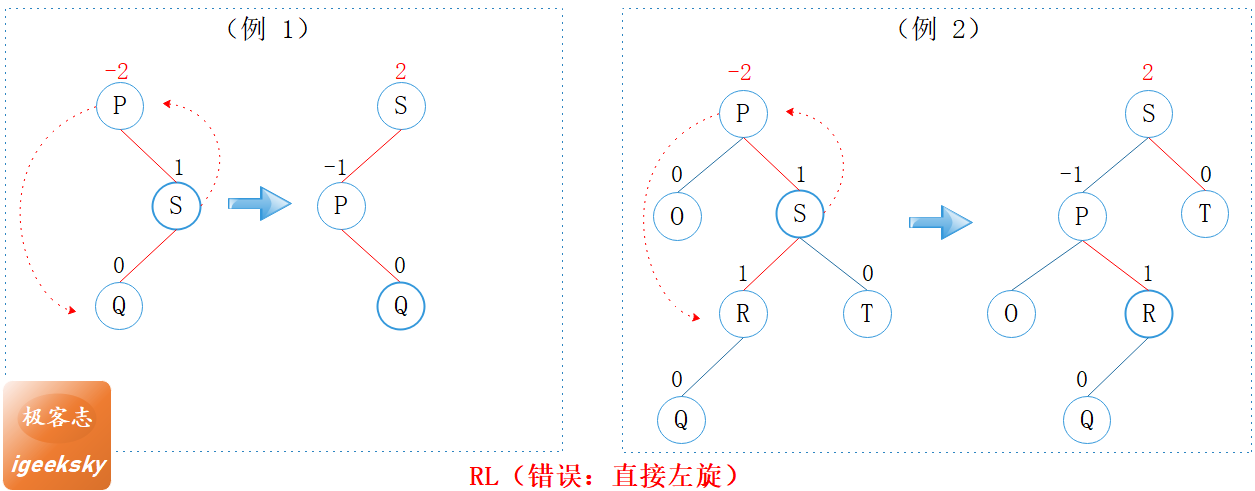
图7: RL型错误示例
观察上图的两个小例子,我们可以发现 P 节点的平衡因子为 -2,右子树更重;其右孩子 S 的平衡因子为 1,左子树更重,因此称为 RL。
其中 P 节点的平衡因子小于 -1,因此需要修正。
对于 RL 型,如上图所示,直接左旋无法恢复平衡性质。
而应该如下图所示,先右旋后左旋。
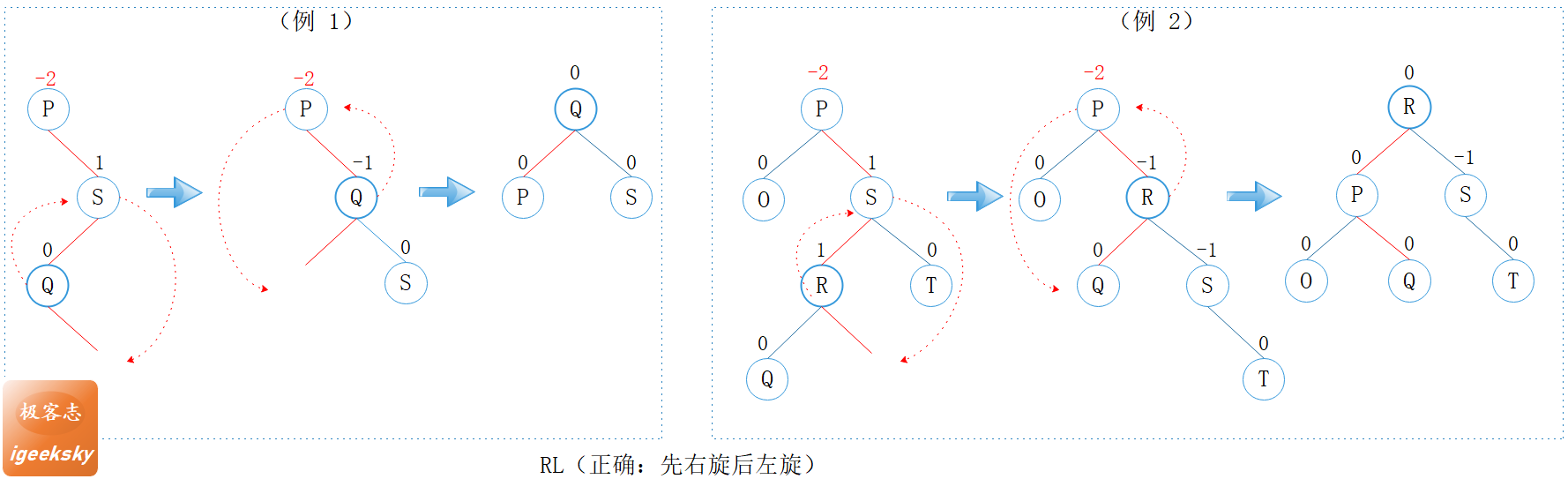
图8: RL型正确示例
private Node<K, V> rotateRightLeft(Node<K, V> parent) {
parent.right = rotateRight(parent.right);
return rotateLeft(parent);
}
3.3. 恢复平衡
根据上面分析,我们可以根据失衡类型来选择如何旋转,使树恢复平衡性质。
private Node<K, V> balance(Node<K, V> parent) {
int factor = balanceFactor(parent);
if (factor >= 2) {
if (balanceFactor(parent.left) <= -1) {
// LR(2, -1):先左旋后右旋
return rotateLeftRight(parent);
}
// LL(2, 1) 或 L(2, 0):右旋
return rotateRight(parent);
} else if (factor <= -2) {
if (balanceFactor(parent.right) >= 1) {
// RL(-2, 1):先右旋后左旋
return rotateRightLeft(parent);
}
// RR(-2, -1) 或 R(-2, 0):左旋
return rotateLeft(parent);
} else {
return parent;
}
}
3.4. 小结
L, LL, R, RR, LR, RL是指失衡类型;左旋、右旋、先左旋后右旋、先右旋后左旋 是指旋转类型。
大多数文章总结了 4 种失衡类型,其实是指 4 种旋转类型。
意识到有 L 型和 R 型的存在,这是理解插入和删除之间区别的关键。后面还会谈到可以根据两者的区别写出性能更优的代码。
4. 查找
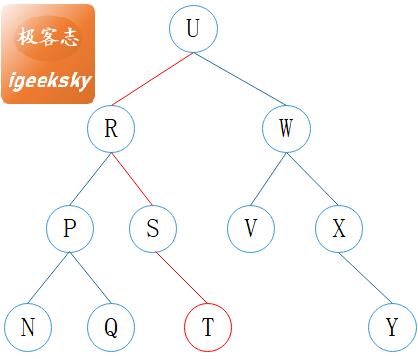
图9:查找
查找的逻辑比较简单,与普通二叉查找树完全一致。
public V get(K key) {
Assert.notNull(key);
Node<K, V> p = root;
while (p != null) {
int cmp = compare(p.key, key);
if (cmp > 0) {
p = p.left;
} else if (cmp < 0) {
p = p.right;
} else {
return p.val;
}
}
return null;
}
5. 插入
与普通二叉查找树相比较,AVL树插入新节点后多了更新高度和恢复平衡的过程。
5.1. 简单例子
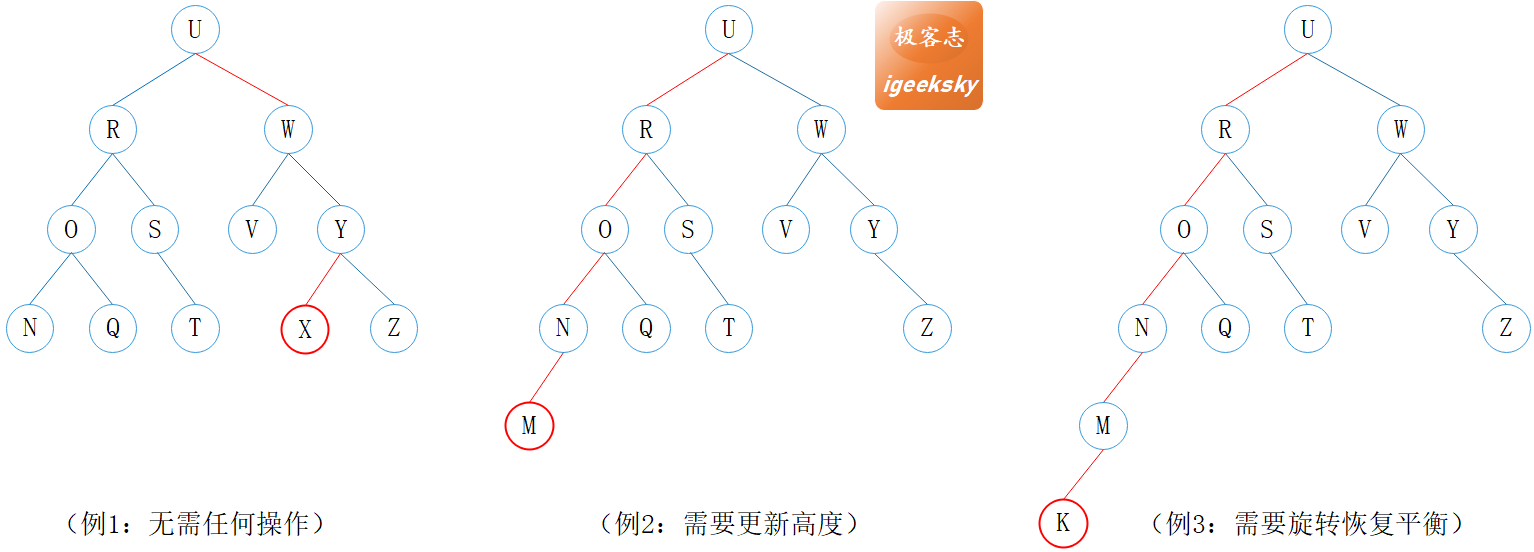
图10:插入
如例1,插入新节点 X 之后,Y 的高度不变,整棵树仍处于平衡状态,则无需任何操作。
如例2,插入新节点 M 之后,N, O, R, U 的高度都会加 1,需从插入节点的父节点开始更新高度直到根节点才结束。
如例3,插入新节点 K 之后,需对 N 进行旋转,旋转完成后,O节点的高度不变,恢复平衡的过程就可以提前终止。
这里给回溯下一个简单的定义:从被修改的节点开始沿父路径递归向上更新节点高度和根据AVL树的平衡性质恢复平衡的过程,称之为AVL树的回溯。
插入节点和删除节点后都需要回溯,例1 可以看作是提前终止回溯的一个特例。
什么情形可以提前终止回溯,是优化 AVL 树插入和删除性能的关键,等后面讲完删除节点之后再来详细分析。
5.2. 代码实现
public void put(K key, V value) {
Assert.notNull(key);
Assert.notNull(value);
if (root == null) {
root = new Node<>(key, value);
size.set(1);
return;
}
Node<K, V> p = root;
int depth = 0, maxDepth = root.height + 1;
// 回溯路径
Node<K, V>[] path = new Node[maxDepth];
while (depth < maxDepth) {
path[depth] = p;
int cmp = compare(p.key, key);
if (cmp > 0) {
if (p.left == null) {
p.left = new Node<>(key, value);
size.increment();
if (p.right != null) {
return; // 父节点高度不变,无需回溯(见例1)
}
break;
} else {
p = p.left;
depth++;
}
} else if (cmp < 0) {
if (p.right == null) {
p.right = new Node<>(key, value);
size.increment();
if (p.left != null) {
return; // 父节点高度不变,无需回溯(见例1)
}
break;
} else {
p = p.right;
depth++;
}
} else {
p.val = value;
return; // 树结构未改变,无需回溯
}
}
// 回溯
root = backtrack(path, depth);
}
6. 删除
AVL 树的删除操作相对复杂一些,我们先看删除流程图,然后再结合例子来讲解。
6.1. 删除流程
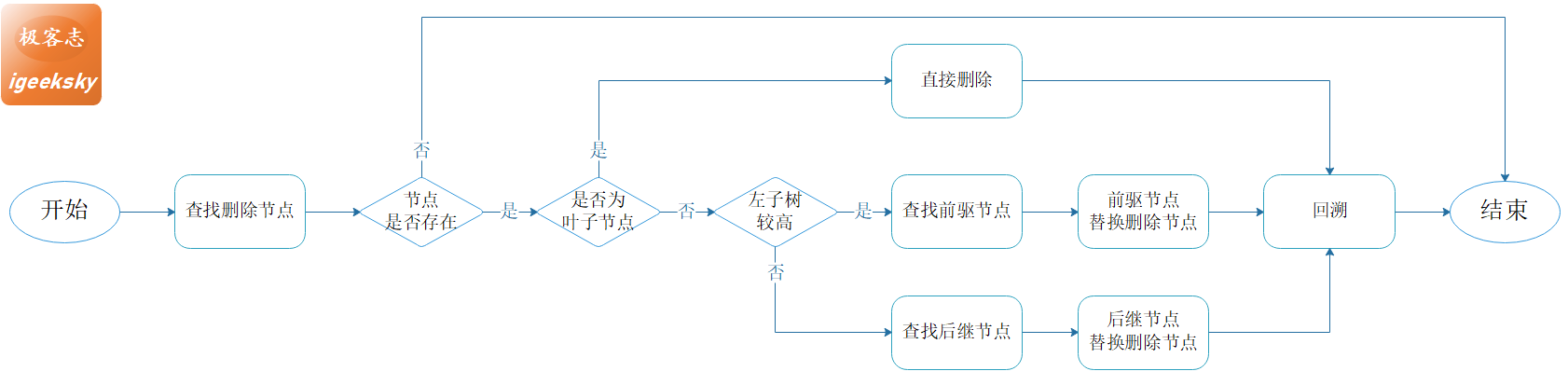
图11:删除流程
流程描述:
- 如果删除节点为叶子节点,直接删除;
- 如果删除节点为非叶节点,左子树较高则用前驱节点替换删除节点;右子树较高则用后继节点替换删除节点;
- 回溯,更新高度并恢复平衡性质。
选择较高子树的节点来替换删除节点是一个小优化,可以减少旋转。
6.2. 简单例子
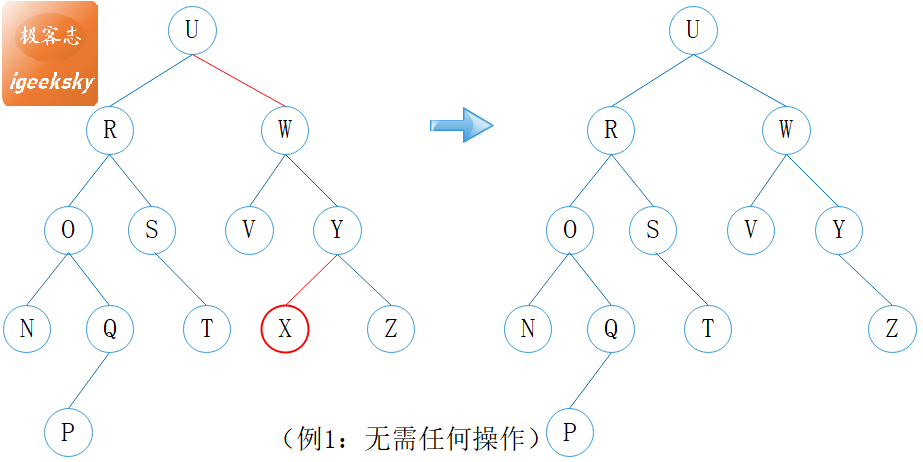
图12:删除-例1
如例1,X 为叶子节点,直接删除。删除节点 X 之后,Y 的高度不变,且 Y 仍处于平衡状态,因此无需任何其它操作。
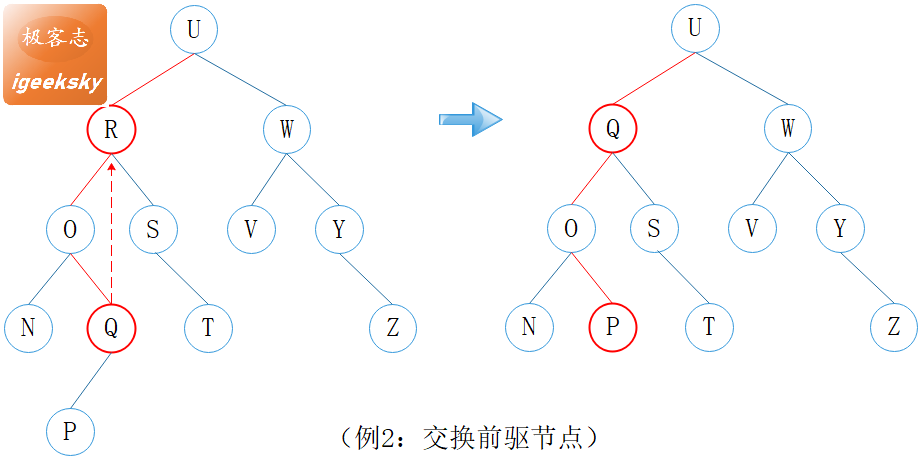
图13:删除-例2
如例2,R 为非叶子节点,R 的左子树较高,找到其前驱节点 Q,然后用 Q 替换 R。替换之后,O, Q, U 的高度都需要更新。
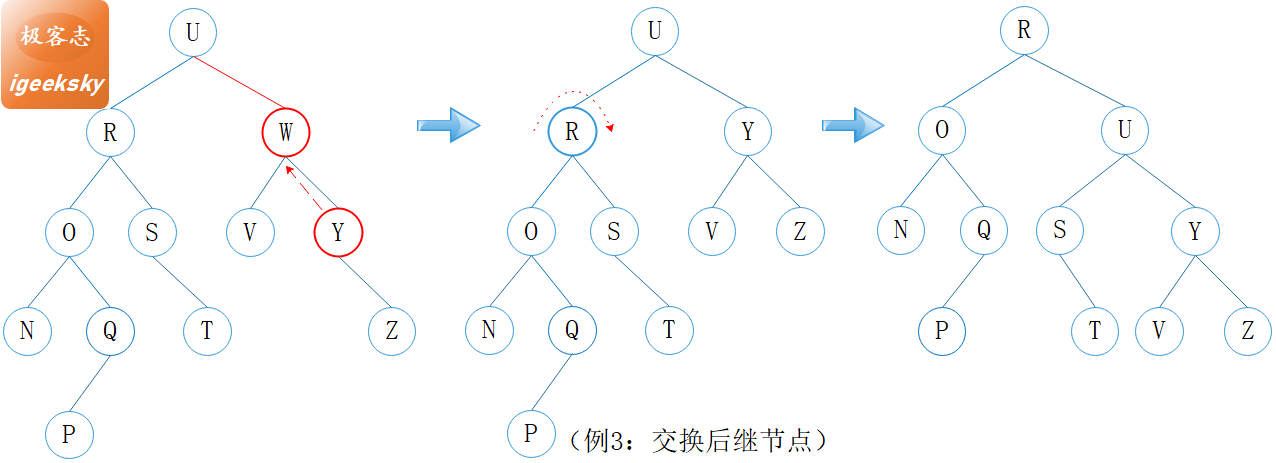
图14:删除-例3
如例3,W 为非叶子节点,W 的右子树较高,找到其后继结点 Y,然后用 Y 替换 W。替换之后,U 处于不平衡状态,旋转恢复平衡。
6.3. 代码实现
public V remove(K key) {
Assert.notNull(key);
if (root == null) {
return null;
}
int depth = 0;
Node<K, V> del = root;
// 根节点至删除节点之间的回溯路径
Node<K, V>[] path = new Node[root.height];
while (del != null) {
int cmp = compare(del.key, key);
if (cmp == 0) {
size.decrement();
if (root == del) {
root = swap(root);
return del.val;
}
Node<K, V> p = path[--depth];
// 节点交换
if (p.right == del) {
p.right = swap(del);
} else {
p.left = swap(del);
}
// 回溯
root = backtrack(path, depth);
return del.val;
}
path[depth] = del;
del = (cmp > 0) ? del.left : del.right;
++depth;
}
return null;
}
节点交换
private Node<K, V> swap(Node<K, V> del) {
Node<K, V> pl = del.left, pr = del.right;
if (height(pl) >= height(pr)) {
if (pl != null) {
// 左子树的高度大于等于右子树:前驱节点交换删除节点
return swapPredecessor(del, pl);
}
//没有子节点
return null;
}
// 右子树的高度大于左子树:后继节点交换删除节点
return swapSuccessor(del, pr);
}
private Node<K, V> swapPredecessor(Node<K, V> del, Node<K, V> swap) {
// 删除节点至交换节点之间的回溯路径
Node<K, V>[] path = new Node[del.height];
int depth = 0;
// 查找前驱节点
while (swap.right != null) {
depth++;
path[depth] = swap;
swap = swap.right;
}
// 替换删除节点
if (depth > 0) {
Node<K, V> p = path[depth];
p.right = swap.left;
swap.left = del.left;
}
swap.right = del.right;
// 回溯
path[0] = swap;
return backtrack(path, depth);
}
private Node<K, V> swapSuccessor(Node<K, V> del, Node<K, V> swap) {
// 删除节点至交换节点之间的回溯路径
Node<K, V>[] path = new Node[del.height];
int depth = 0;
// 查找后继节点
while (swap.left != null) {
depth++;
path[depth] = swap;
swap = swap.left;
}
// 替换删除节点
if (depth > 0) {
Node<K, V> parent = path[depth];
parent.left = swap.right;
swap.right = del.right;
}
swap.left = del.left;
// 回溯
path[0] = swap;
return backtrack(path, depth);
}
7. 回溯
回溯代码非常简单,就是沿父路径循环向上更新高度和恢复平衡,需要考虑的是什么情形可以提前终止回溯。
7.1. 代码实现
private Node<K, V> backtrack(Node<K, V>[] path, int depth) {
for (int j = depth; j > 0; j--) {
Node<K, V> p = path[j];
Node<K, V> pp = path[j - 1];
int height = p.height, newHeight;
updateHeight(p);
if (pp.left == p) {
pp.left = balance(p);
newHeight = pp.left.height;
} else {
pp.right = balance(p);
newHeight = pp.right.height;
}
if (newHeight == height) {
break; // 高度不变,停止回溯(见命题1 的证明)
}
}
updateHeight(path[0]);
return balance(path[0]);
}
7.2. 回溯分析
命题
AVL树插入或删除一个节点后,回溯过程中任意一个节点的高度无变化且其已处于平衡状态,则无需继续回溯。
证明:
AVL树的回溯是为了更新节点高度和恢复平衡性质。
回溯过程是沿回溯路径从深度最大的节点向根节点循环顺序调整,那么已回溯的节点必定已更新高度和恢复平衡性质。
设 X 为回溯路径中的任意一个节点,X 的高度无变化且已处于平衡状态,那么未回溯调整的剩余节点均为其祖先节点。因此要证明命题为真,只需证明两点:
- X 的所有祖先节点的高度和平衡因子均无变化;
- X 的所有祖先节点已处于平衡状态。
二叉搜索树增删一个节点,仅可能改变回溯路径中的节点的高度。
即当一个节点处于回溯路径中,该节点的父节点的另一个孩子高度一定不变。因此,当 X 高度无变化时:根据二叉树高度的定义,其父节点的高度一定不变;根据平衡因子的定义,则父节点的平衡因子也一定不变。同理,其父节点的父节点高度和平衡因子也不变,由此可得 X 的所有祖先节点的高度和平衡因子均无变化。
这就证明了1。
AVL树的任意节点在增删一个节点之前,一定处于平衡状态,一个节点的平衡因子不变则表示该节点依然处于平衡状态。
结论1 已证明 X 的所有祖先节点的平衡因子不变,因此其所有祖先节点一定依然处于平衡状态。
这就证明了2。
由此得证。
证明过程有点啰嗦,其实可以“显然”的😀。
问题
命题1 的证明已说明了回溯代码的正确性,我们再来深入思考一些常见问题,看看是否可以继续优化。
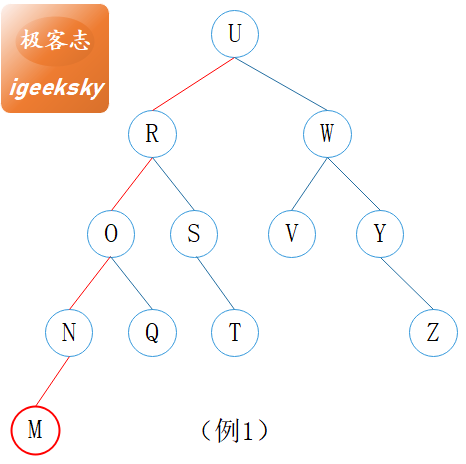
图15:回溯更新高度
(1) AVL树插入一个节点,最坏情况下需要 \( log_2n \) 次的高度更新(需要回溯到根节点)。
如例1 所示,插入节点M。当根节点的左右子树高度相同,新插入节点的父节点是树中深度最大的节点之一,且插入节点后树中所有节点依然保持平衡性质。
这意味着其所有祖先节点的高度都需要加1,所以需要 \( log_2n \) 次的高度更新。
(2) AVL树删除一个节点,最坏情况下需要 \( log_2n \) 次的高度更新(需要回溯到根节点)。
如例1 所示,删除节点 M。当删除唯一深度最大的叶子节点,且删除节点后树中其它节点依然保持平衡性质。
这会导致其所有祖先节点的高度都需要减1,所以需要 \( log_2n \) 次的高度更新。
(3) AVL树插入一个节点,最多仅需一次旋转即可恢复其平衡性质(一次单旋转或一次双旋转)。
AVL树的失衡类型一共有6种,L 型和 R 型仅在删除节点时才会出现,因此我们只需考虑 LL、RR、LR 和 RL 这4种失衡类型。
插入一个节点最多使得新节点所在的子树的高度加1,而LL、RR、LR 和 RL 这4种类型触发的旋转总是会将新节点所在子树的高度减1。
因此,AVL树插入一个节点,最多仅需一次旋转即可恢复其平衡性质。
(4) AVL树删除一个节点,最坏情况下需要 \( log_2n \) 次旋转才能恢复平衡性质(需要回溯到根节点)。
插入节点是子树高度加1,旋转会将子树高度减1,因此一次旋转即可恢复平衡;
删除节点是子树高度减1,旋转可能会将高度再次减1,这可能会触发再次旋转。
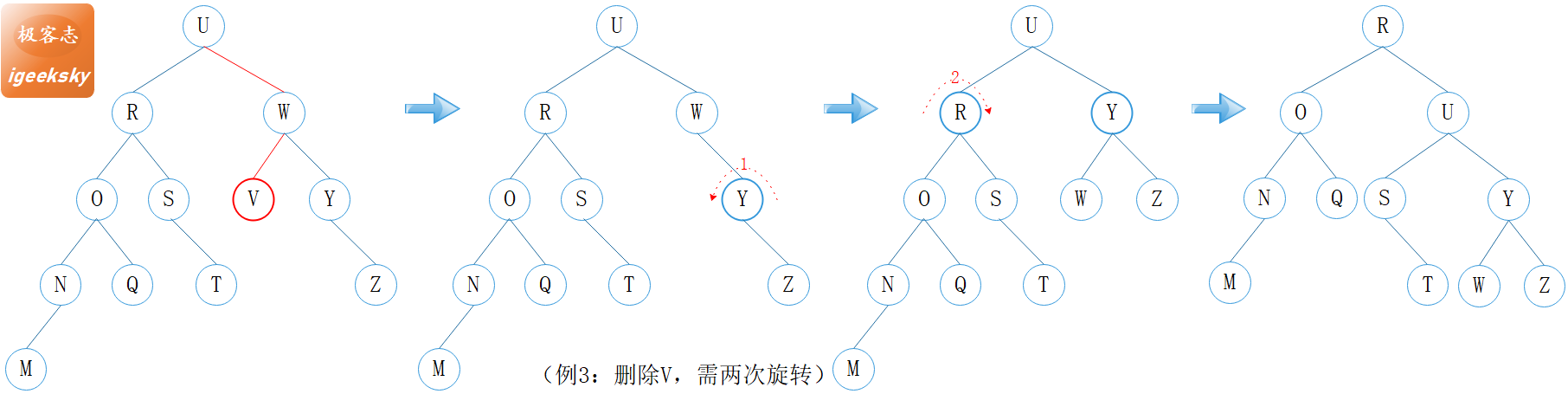
图16:多次旋转1
如例 3 所示:
W 的初始平衡因子为 -1,U 的平衡因子为 +1;
当删除 V 之后,W 的平衡因子变为 -2,触发第1次旋转;
第 1 次旋转完成之后,U 的平衡因子变为 2,触发第2次旋转。
我们可以用一个比较抽象的方式来表示这个规律:
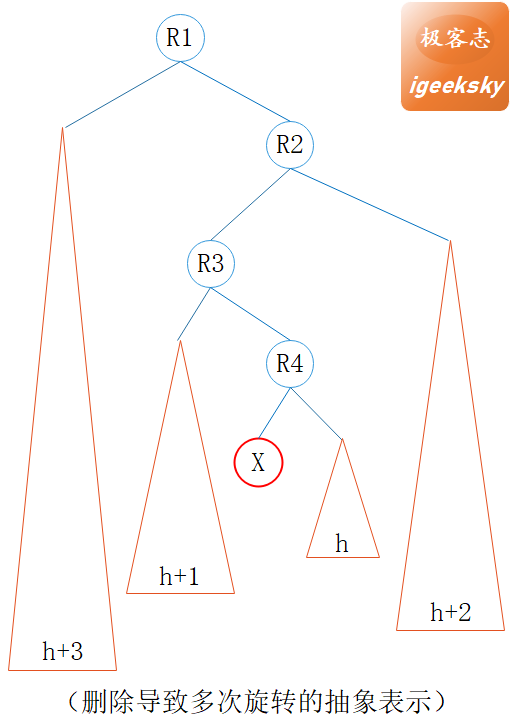
图17:回溯多次旋转2
删除节点 X 之后,R4的平衡因子变为 -2,R4 左旋;R3 的平衡因子变为 2,R3 右旋;R2 的平衡因子变为 -2, R2左旋;R1的平衡因子变为2,R1 右旋……
当从根节点至待删除节点的父节点平衡因子交替为 -1 和 +1,删除该节点一旦触发旋转就需要 \( log_2n \) 次旋转(回溯至根节点)。
结论
新增或删除一个节点,高度更新可能需要回溯到根节点;新增一个节点,最多仅需一次旋转;删除一个节点,旋转可能需要回溯到根节点。
根据这个结论,如果追求极致性能的话,其实可以区分新增节点和删除节点的回溯代码:对于新增节点的情形,只要触发一次旋转就不再继续回溯。
我不想写两段回溯代码,也不想加判断条件,代码变丑又没有大的性能改进,所以就先这样喽。
8. 性能对比
随机生成1000万长度为6~9的字符串,AvlTree 与 Java 标准库中的 TreeMap(红黑树) 进行插入和查找的性能对比,测试结果如下(毫秒):
# 测试平台
# CPU:Intel(R) Core(TM) i9-7900X CPU @ 3.30GHz
# RAM:64G DDR4(3000 MHz)
# OS:Win10(21H1)
# JDK:11.0.5
avl-put: 16340
map-put: 15000
avl-get: 12127
map-get: 12872
多次运行的测试结果类似。
相比红黑树,AVL树的插入稍慢查找略快,但两者差别非常小,这也符合算法分析的结果。
参考资料
G. Adelson-Velsky & E. M. Landis. An Algorithm for the Organization of Information. Proc. of the USSR Academy of Sciences (1962), 146:263-266 ↩︎