1. 前言
红黑树是一种自平衡二叉查找树(Self-balancing binary search tree)。
如前文所述,根据红黑树的定义去理解其设计思想是非常困难的,但借助 B 树我们却可以更好地理解它,因为红黑树本就是由4阶B树推导而来。
全文较长,但为了完整的阅读体验,所以没有拆分为多篇文章,读者可以根据导图挑选阅读感兴趣的章节。
代码仓库:https://github.com/patricklaux/perfect-code
2. 由来
了解红黑树的由来和变体,有助于更好地理解。
(1) 1972 年,Rudolf Bayer 提出了 “symmetric binary B-tree”,这是B 树的 4 阶情形,也就是 2-3-4树(或称为 2-4 树)1。
(2) 1978 年,Leonidas J. Guibas 和 Robert Sedgewick 从 “symmetric binary B-tree” 推导出红黑树2。
(3) 1993 年,Arne Andersson 引入 “right leaning tree(右倾树)” 的概念来简化插入和删除操作3。
(4) 1999 年,Chris Okasaki 展示了如何使插入操作成为纯函数,只需处理 4 种失衡类型和 1 种默认平衡类型4。
(5) 2001 年,Cormen 等人将原算法的 8 个失衡类型减少为 6 个失衡类型5。
(6) 2008 年,Sedgewick 根据 Andersson 的思想,提出了 “Left leaning red black tree(左倾红黑树)”,这是 2-3 树的等价转换6。
因此,红黑树现在主要有两个流行版本:
版本一:根据 4 阶 B 树( 2-3-4 树)转换而来的红黑树;
版本二:根据 3 阶 B 树( 2-3 树)转换而来的左倾红黑树。
因为 Java 中的 TreeMap 是版本一的实现,所以我将介绍版本一。
不过,道理是相通的,理解了版本一,也就理解了版本二,版本二只是通过增加 “红链接均为左链接” 这一性质来简化实现而已。
另外,Java 中的 TreeMap 在 JDK1.2 时就已存在(1998年),因此插入和删除的实现其实并不那么简洁优美。
所以,我根据《算法导论.第3版》7 又重新实现了一遍,并且再稍稍优化了部分逻辑,使之更加清晰可读。
3. 性质与概念
性质
红黑树是一棵二叉查找树,有五个基本性质:
(1) 节点要么是红色,要么是黑色;
(2) 根节点是黑色的;
(3) 每个外部节点(nil 节点)是黑色的;
(4) 每个红色节点的两个子节点都是黑色的;
(5) 从任一个节点到其外部节点的所有路径包含相同数量的黑色节点。
概念
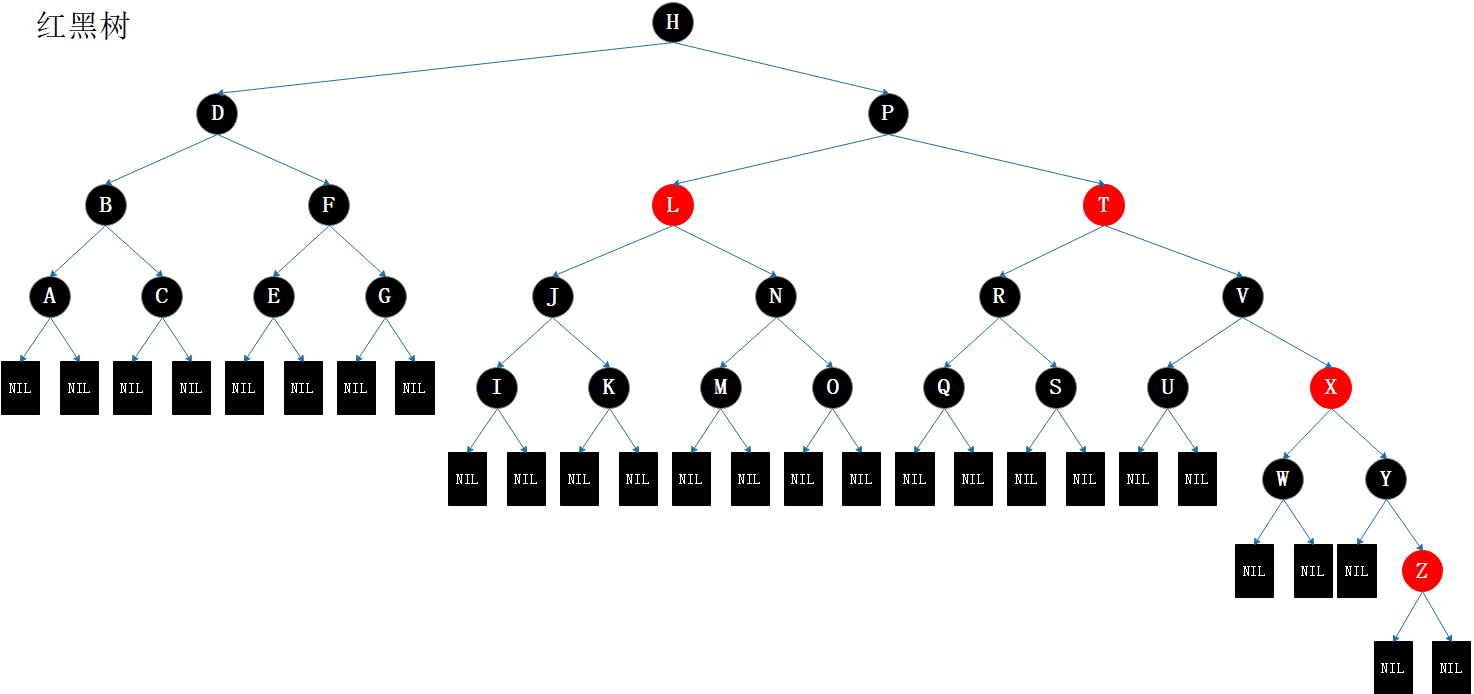
图3.1 红黑树
外部节点
外部节点没有键和子节点,即图3.1中的NIL节点(见参考资料1)。
红黑树中通常用空指针或一个特殊的哨兵节点来指代。
内部节点
内部节点包含一个键和两个子节点,这两个子节点可以是外部节点(见参考资料1)。
叶子节点
叶子节点指的是包含键的最底层节点。
《算法导论.第2版》5中关于红黑树的描述:叶子节点即外部节点。
这里与前文 B 树介绍中的概念保持一致:叶子节点并非是外部节点。
高度
红黑树的高度最大为 \( 2log_2(n+1) \)。
性质4 和 5 限制了红黑树高度的最大值,因此这两点是关键性质,后面介绍的插入和删除后的修复,几乎都是为了维护这两点。
我们先理解红黑树及相关操作,最后再来证明这个命题。
黑高(black height)
红黑树的黑高是指从根到外部节点的任一路径上的黑色节点的数量。
根据性质 5 ,根到任一外部节点的路径上的黑色节点数都必定是相等的。
如图3.1,以 H 为根的红黑树其黑高为 4,以 P 为根的子树的黑高为3,以 T 为根的子树的黑高也为3……
黑深(black depth)
一个节点的黑色深度是指从根到该节点的黑色节点的数量(即其黑色祖先数量)。
如图3.1,H 的黑深为0,P 的黑深为1,L 的黑深为2,W的黑深为3,Z的黑深为4,所有外部节点的黑深均为4。
红色违规
违反性质4。
黑色违规
违反性质5。
4. 等价转换
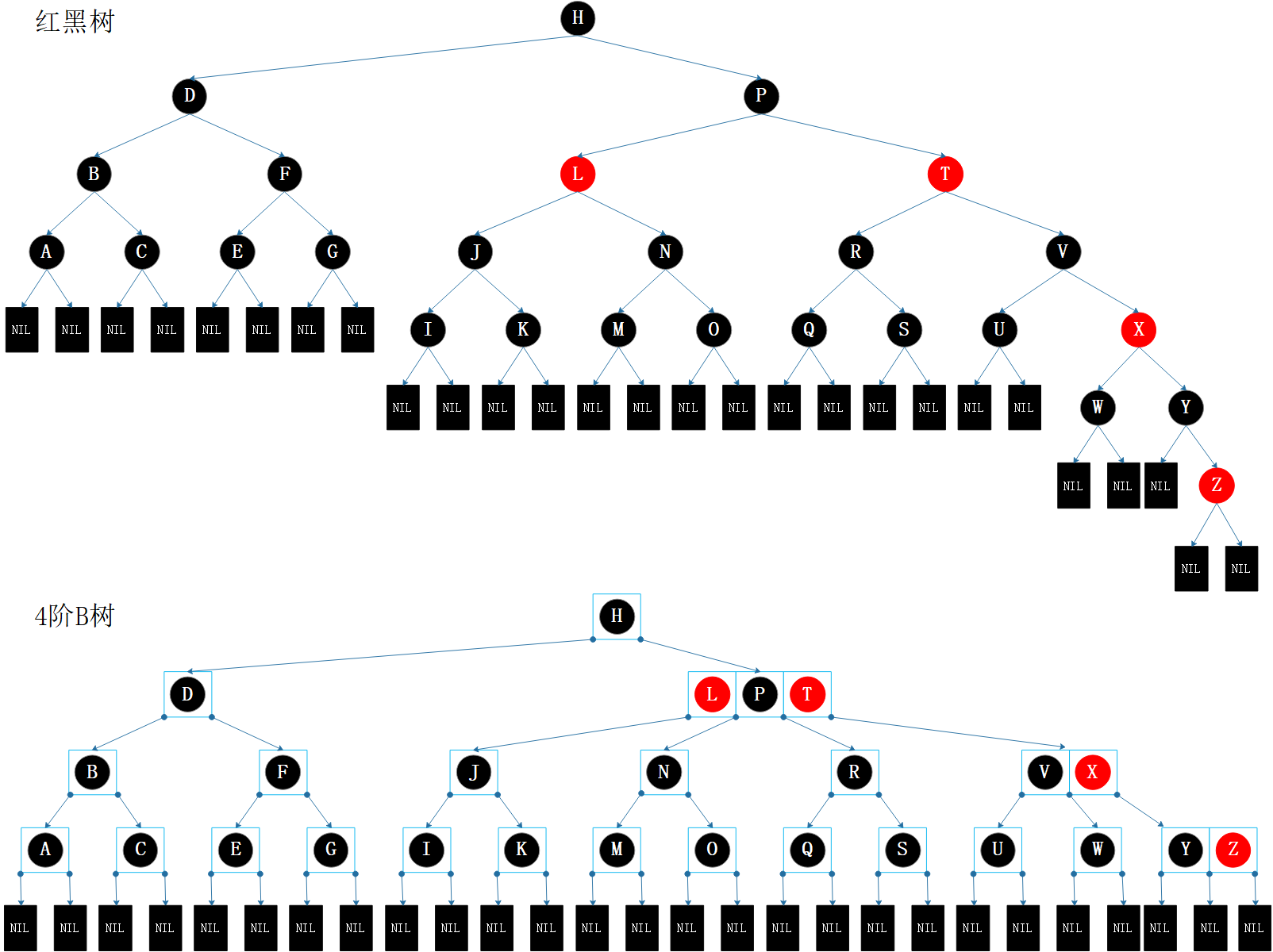
图4.1 等价转换
观察图4.1,我们会发现:
- 红黑树的红色节点提升一层与其父节点合并,就可得到一棵 4阶B树。
- 红黑树的黑高正好是 4阶B树的高度。
4阶B树转换为红黑树
- 4-节点拆分成1个黑色父节点和2个红色子节点:正中间的键对应节点为黑色,在两边的键对应节点为红色,如【L P T】。
- 3-节点拆分成1个黑色父节点和1个红色子节点:先插入的键对应节点为黑色,后插入的键对应节点为红色,如【V X】和【Y Z】。
- 2-节点全部转换成黑节点。
4-节点:4 个孩子 3 个键;3-节点:3 个孩子 2 个键;2-节点:2 个孩子 1 个键。
5. 节点定义
class Node<K, V> {
K key; // 键
V val; // 值
Node<K, V> left; // 左孩子
Node<K, V> right; // 右孩子
Node<K, V> parent; // 父节点
boolean red = RED; // 颜色,默认红色
Node(K key, V value, Node<K, V> parent) {
this.key = key;
this.val = value;
this.parent = parent;
}
Node(K key, V value, boolean red) {
this.key = key;
this.val = value;
this.red = red;
}
}
6. 插入
6.1. 流程
插入操作相对复杂,因此分为两个流程:主流程描绘整体逻辑;子流程描绘性质修复。
6.1.1. 主流程
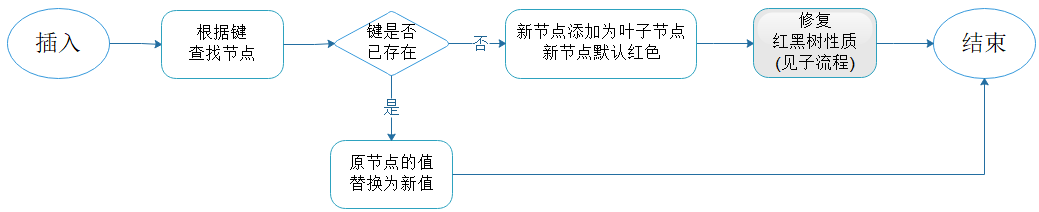
图6.1 插入主流程
6.1.2. 子流程
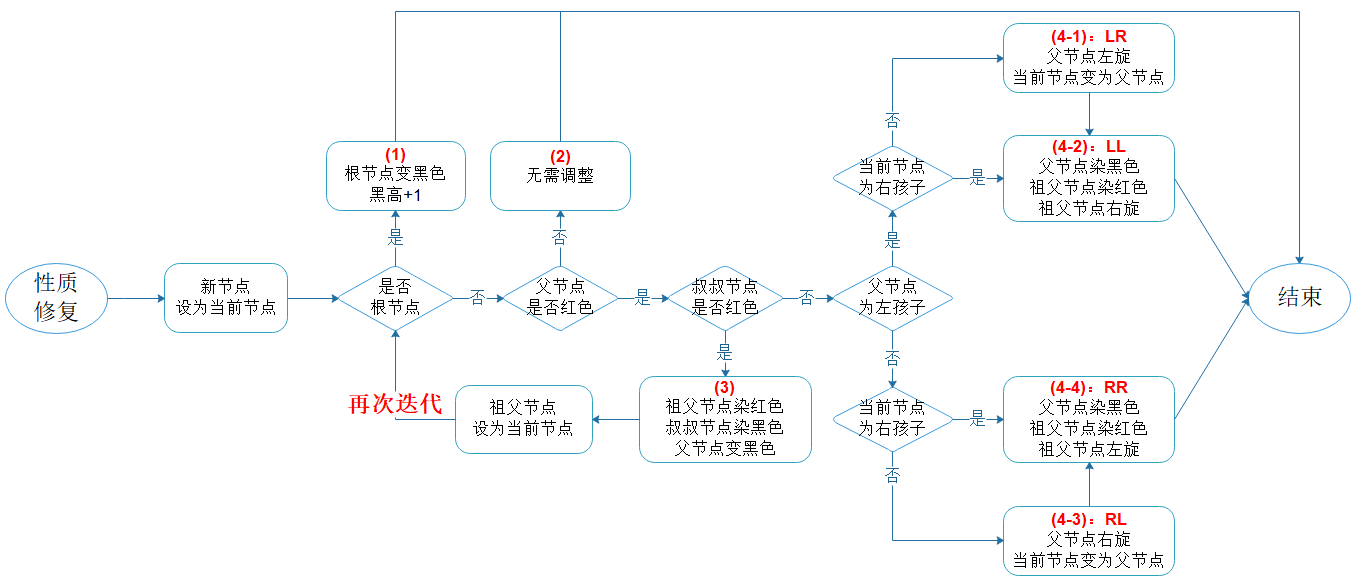
图6.2 性质修复子流程
流程说明:
- 根节点由红变黑,红黑树的黑高加 1;
- 父节点为黑色,这是默认平衡情形,无需调整;
- 父节点为红色,叔叔节点为黑色,最多两次旋转即恢复平衡;
- 只有父节点和叔叔节点都为红色,才需要再次迭代。
具体可以先看下图,然后再结合代码和流程图来理解。
6.1.3. 情形分析
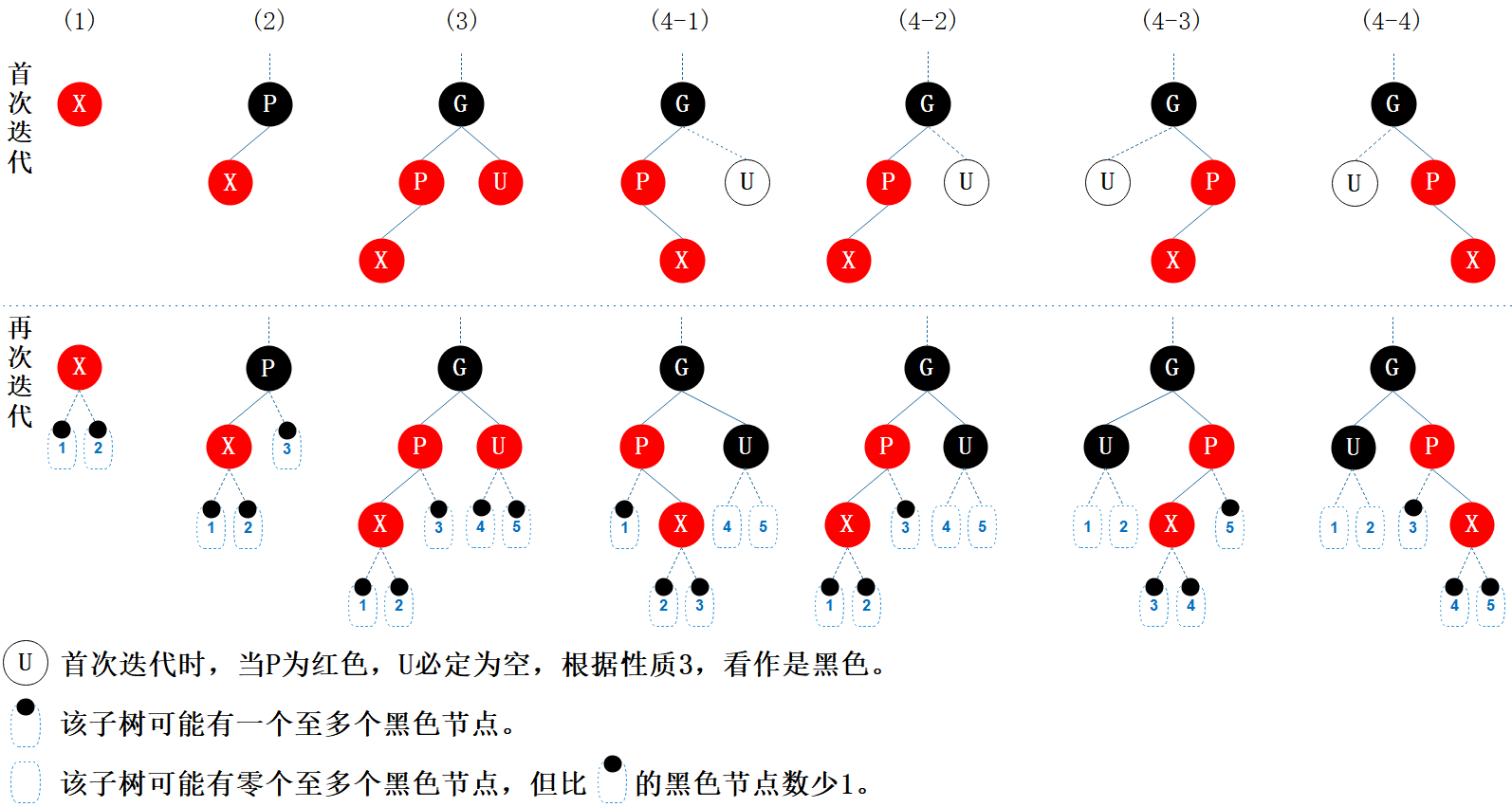
图6.3 插入情形概览
如上图所示,红黑树的插入,可以枚举出以下四种情形:
(1) 当前节点为根节点;
(2) 父节点为黑色;
(3) 父节点为红色,叔叔节点为红色;
(4) 父节点为红色,叔叔节点为黑色;
(4-1) LR:父节点为祖父节点的左孩子,当前节点为父节点的右孩子;
(4-2) LL:父节点为祖父节点的左孩子,当前节点为父节点的左孩子;
(4-3) RL:父节点为祖父节点的右孩子,当前节点为父节点的左孩子;
(4-4) RR:父节点为祖父节点的右孩子,当前节点为父节点的右孩子。
6.2. 性质修复
(1) 当前节点为根节点
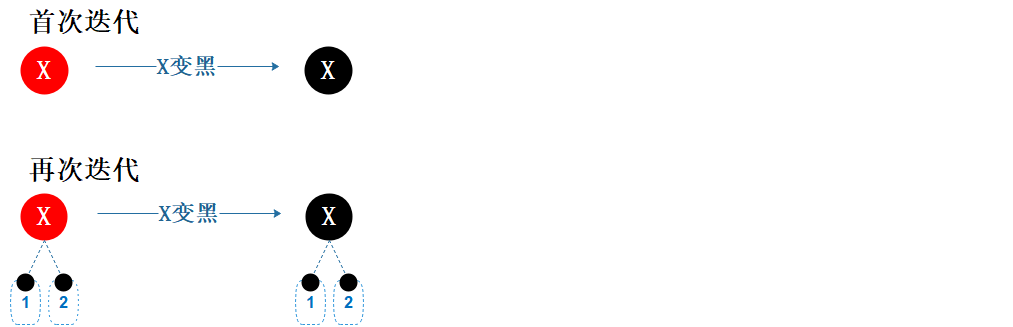
图6.4 性质修复1
根节点为红色,违反性质2。
演化:
首次迭代:(1)
再次迭代:(3) —> (1)
操作:
当前节点 X (即根节点) 染成黑色,性质 2 被满足,同时不违反其它性质,结束。
这种情况下,相当于是从根节点到任意外部节点的黑色节点的数量都加 1,即树的黑高加 1。
说明:如果是首次迭代,X 无孩子;如果是再次迭代,即由情形3 演化而来时,X 有两个黑孩子。
演化的意思是可能由哪种情形演变成此种情形。
(2) 父节点为黑色

图6.5 性质修复2
这是默认的平衡情形,没有违反红黑树的任何性质,无需调整,结束。
演化:
首次迭代:(2)
再次迭代:(3) —> (2)
说明:如果是首次迭代,X 无孩子;如果是再次迭代,即由情形3 演化而来时,X 有两个黑孩子,子树3 有至少1个黑节点。
(3) 父节点为红色,叔叔节点为红色
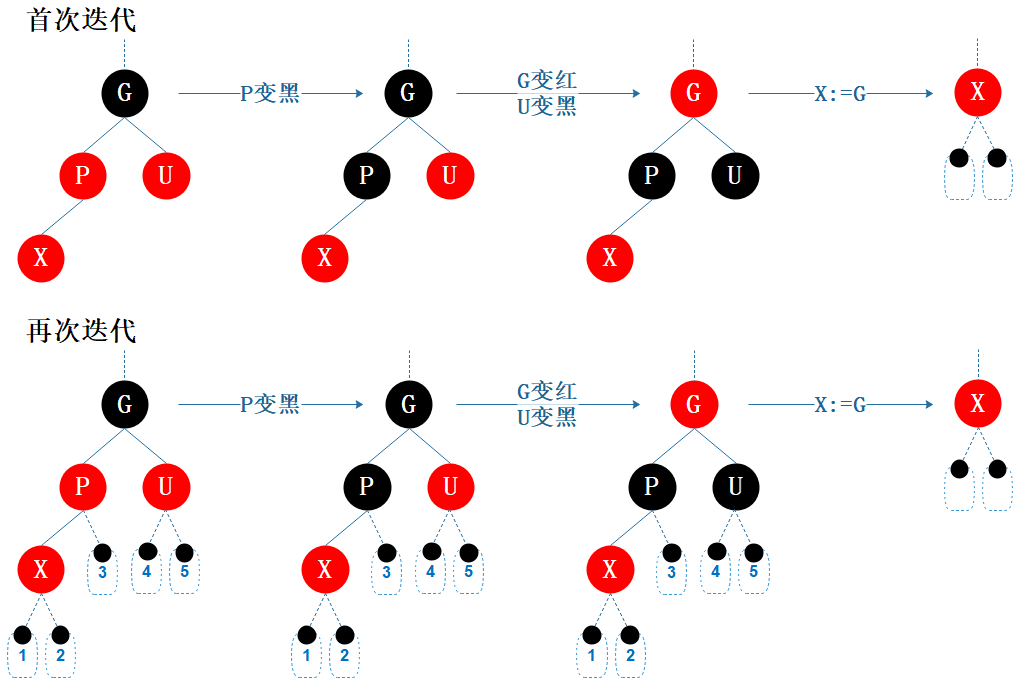
图6.6 性质修复3
父节点 P 和当前节点 X 均为红色,违反性质4。
演化:
首次迭代:(3)
再次迭代:(3) —> (3)
操作:
父节点 P 染黑色,性质4被满足,但又违反了性质5:从根节点到经过 P 的路径上的黑色节点数比其它路径多1;
再将祖父节点 G 染红色,叔叔节点 U 染黑色,性质5 被满足;
最后将祖父节点设为当前节点,未结束。
后续:
如果新 X 已经是根节点,那么就会演变成情形 1。
如果新 X 仍然有父节点,那么就会演变成情形 2、情形 3 或情形 4;最坏的情况下,一直都是情形3,那么需要递归向上处理直到根节点才结束。
(4) 父节点为红色,叔叔节点为黑色
(4-1) LR:父节点为祖父节点的左孩子,当前节点为父节点的右孩子
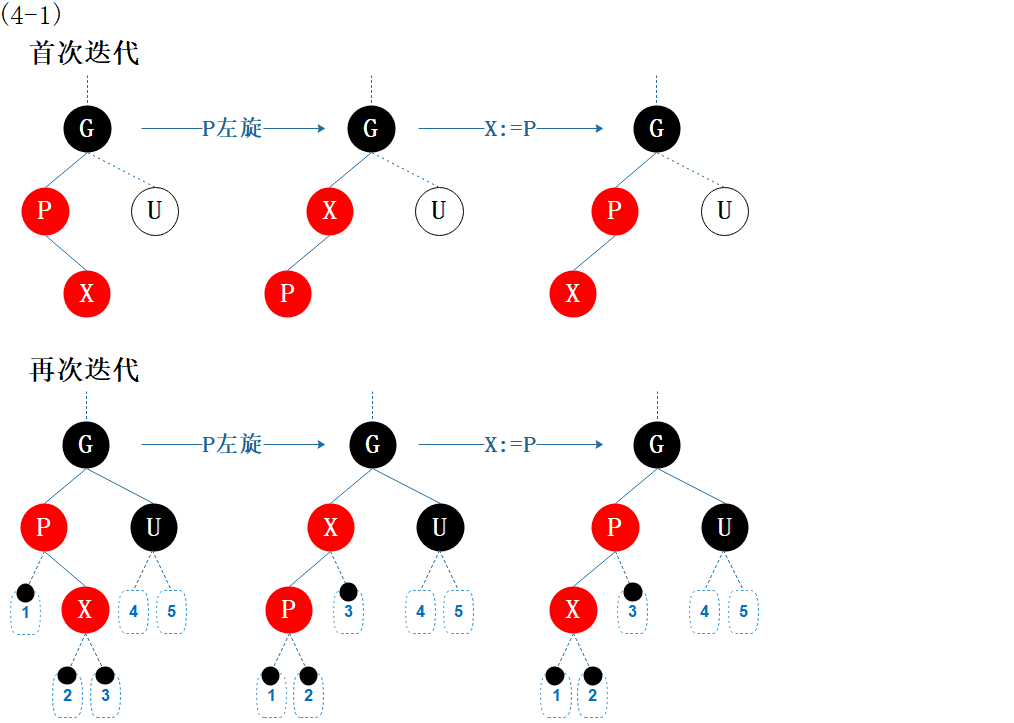
图6.7 性质修复4-1
父节点 P 和当前节点 X 均为红色,违反性质4。
演化:
首次迭代:(4-1)
再次迭代:(3) —> (4-1)
操作:
父节点 P 左旋转换成 (4-2)LL 型,旋转后 X 成了 P的父节点,因此再将父节点设为当前节点。
性质4 仍然未满足,未结束。
后续:根据 (4-2) LL 进行处理。
(4-2) LL:父节点为祖父节点的左孩子,当前节点为父节点的左孩子
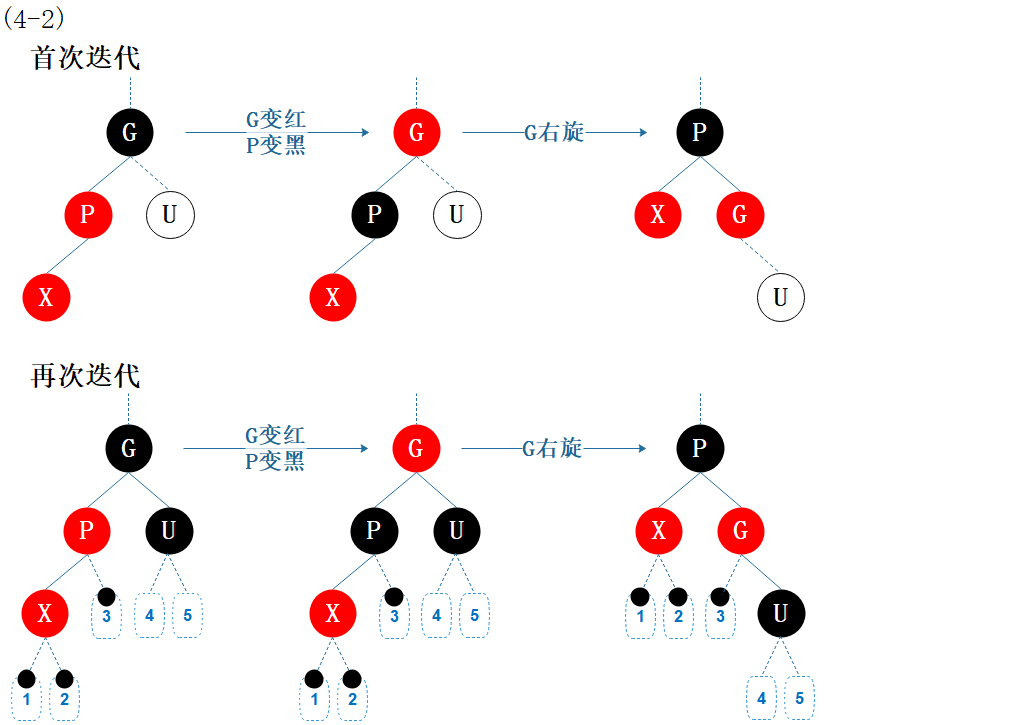
图6.8 性质修复4-2
父节点 P 和当前节点 X 均为红色,违反性质4。
演化:
首次迭代:(4-1);(4-1) —> (4-2)
再次迭代:(3) —> (4-1);(3) —> (4-1) —> (4-2)
操作:
父节点染黑色,祖父节点染红色,性质 4 被满足,但又违反了性质 5:经过 U 的路径上的黑色节点数比其它路径少 1;
祖父节点 G 右旋,性质 5 被满足,结束。
(4-3) RL:父节点为祖父节点的右孩子,当前节点为父节点的左孩子
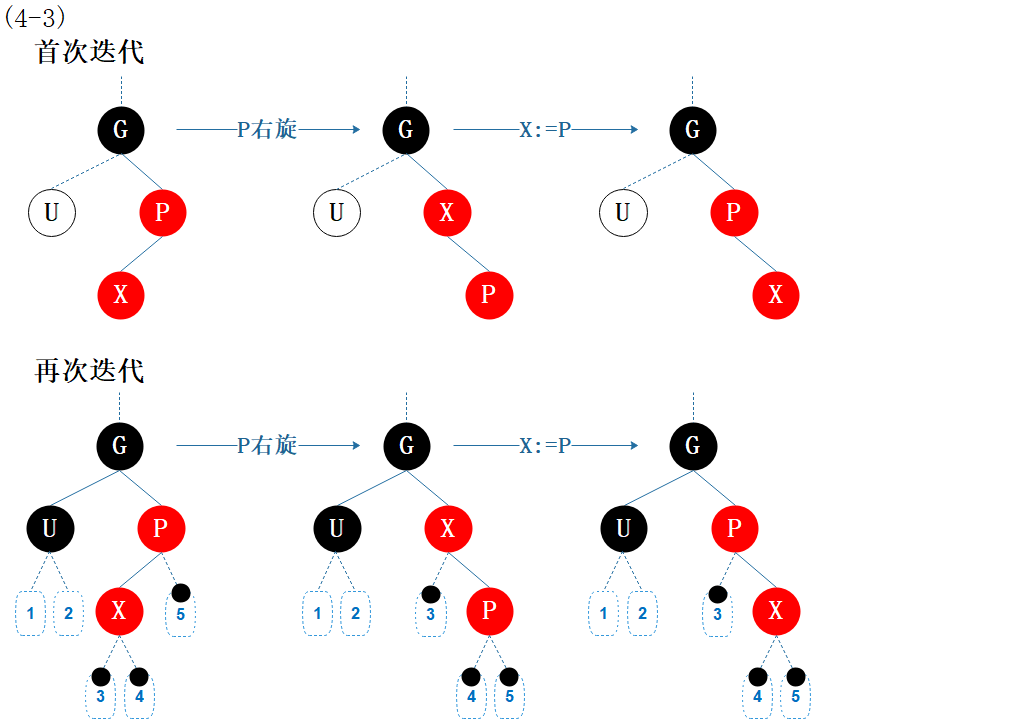
图6.9 性质修复4-3
这是 (4-1)LR 的对称情形,略。
(4-4) RR:父节点为祖父节点的右孩子,当前节点为父节点的右孩子
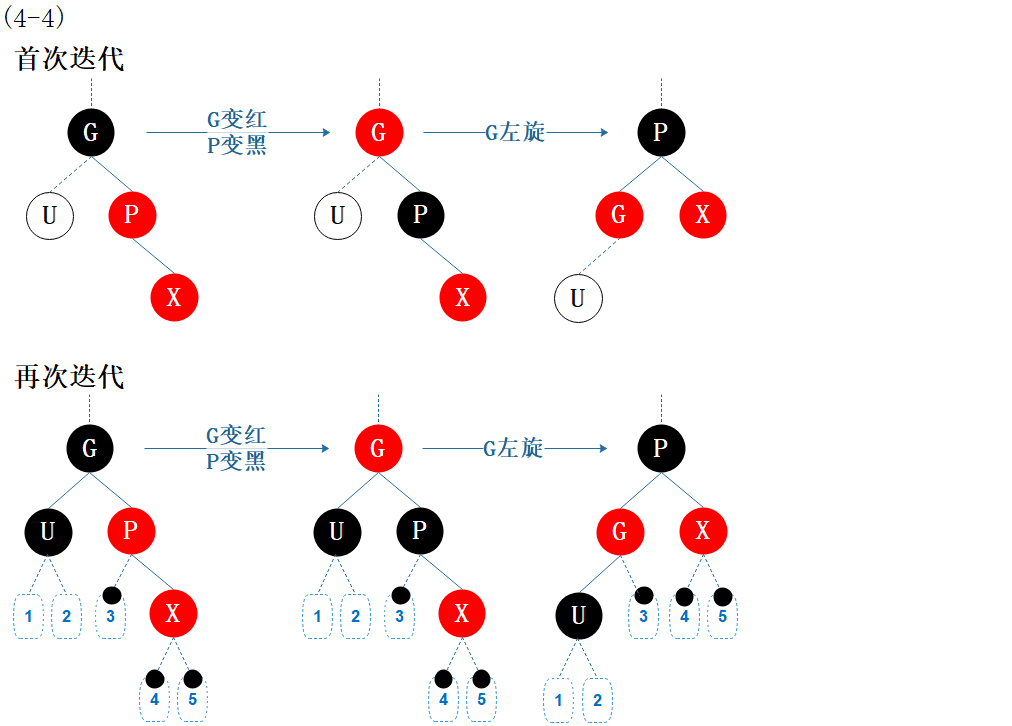
图6.10 性质修复4-4
这是 (4-2)LL 的对称情形,略。
6.3. 操作等价性
这一小节,我们来探讨红黑树和4 阶 B 树关于插入操作的等价关系。
看完这些示例,相信会对为什么要考察父节点和叔叔节点的颜色有更深的理解。
无上溢
4 阶 B 树的一个内部节点最多有3个键,2-节点再插入一个键,3-节点再插入一个键,都不会出现上溢。
4 阶 B 树的 2-节点再插入一个键变成 3-节点,对应到红黑树是默认平衡情形,肯定不用调整。
4 阶 B 树的 3-节点再插入一个键变成 4-节点,则需看插入的先后顺序,对应红黑树中的旋转。
(中 —> 小 —> 大)或(中 —> 大 —> 小):红黑树中,父节点为黑色,默认平衡情形,无需调整;
(大 —> 中 —> 小)或(小 —> 中 —> 大):红黑树中,父节点为红色,叔叔节点为黑色,对应需要 1 次旋转 (LL,RR);
(大 —> 小 —> 中)或(小 —> 大 —> 中):红黑树中,父节点为红色,叔叔节点为黑色,对应需要 2 次旋转 (LR,RL);
这里只画了(小 —> 中 —> 大)( G H I ) 这种插入顺序,其它情形略。
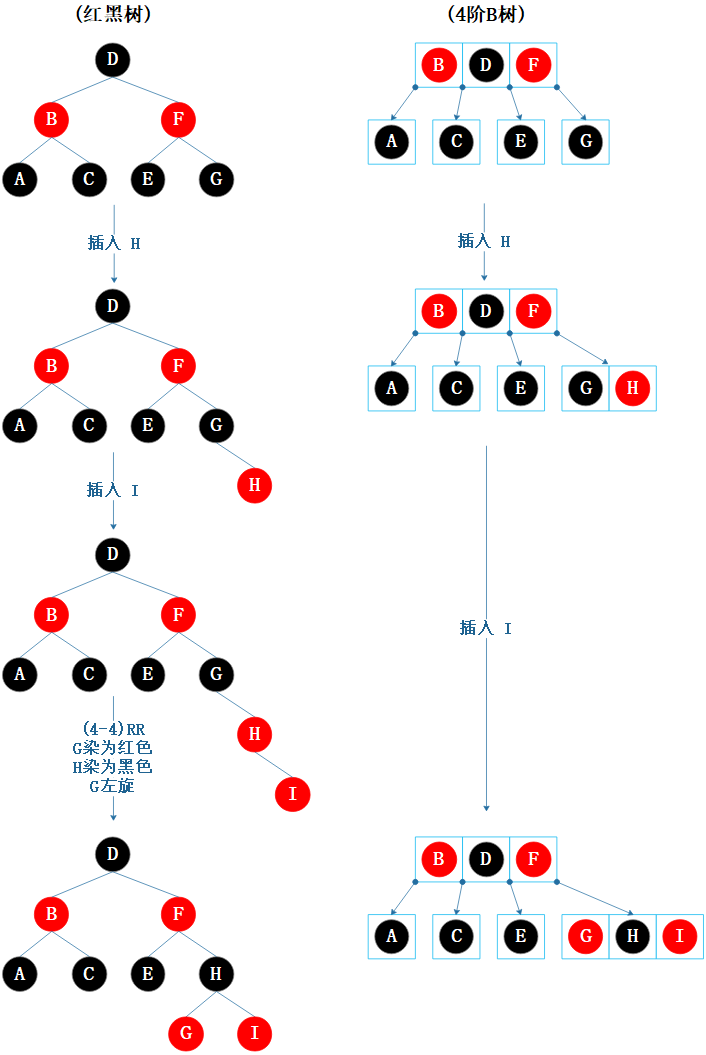
图6.11 等价操作示例1
上溢
4 阶 B 树的 4-节点再插入 1个键,会出现上溢问题,需通过分裂来修复。
等价于红黑树新节点的父节点和叔叔节点均为红色,需通过变色来修复。
最坏情况下,两者都需要递归向上处理直到根节点才结束。
如果递归到根节点,那么,4 阶 B 树的高度会加 1,相应地红黑树的黑高也加 1。
接上图,继续插入 J。
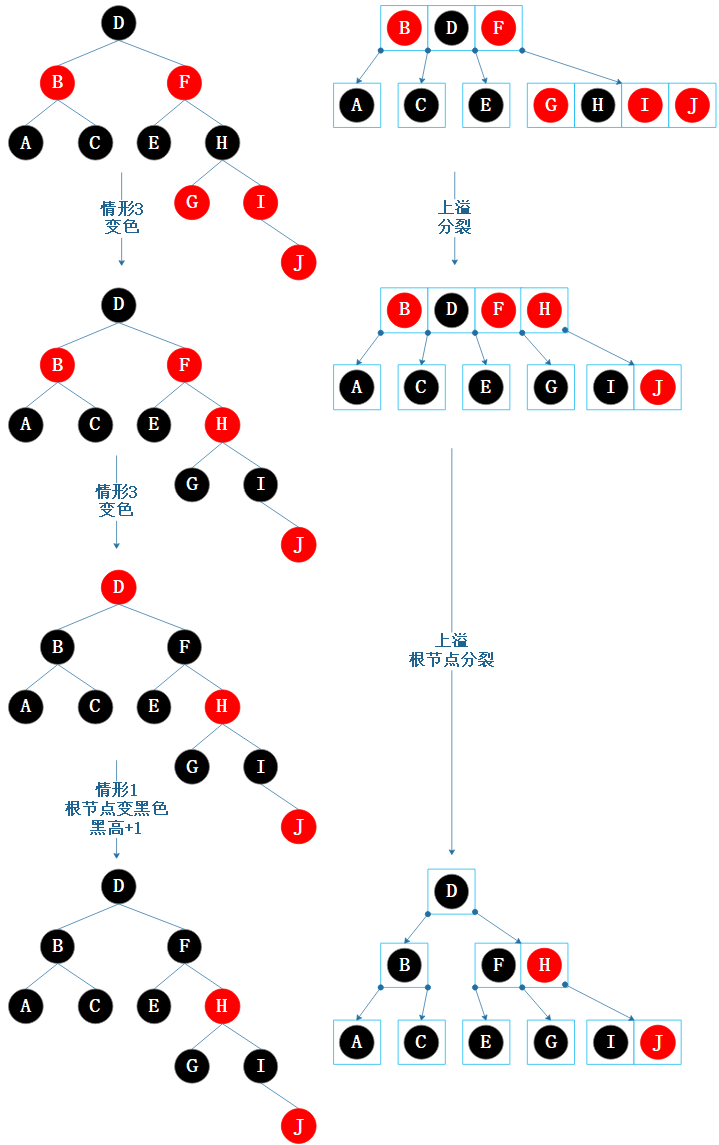
图6.12 等价操作示例2
6.4. 代码实现
代码逻辑与流程图一致,可与之相互印证理解。
6.4.1. 插入
public void put(K key, V value) {
Assert.notNull(key);
Assert.notNull(value);
// 情形1:新插入节点为根节点
if (root == null) {
size.increment();
root = new Node<>(key, value, BLACK);
size.set(1);
return;
}
Node<K, V> p = root;
// 先查找,并将新节点添加为叶子节点
while (true) {
int cmp = compare(p.key, key);
if (cmp > 0) {
if (p.left == null) {
size.increment();
p.left = new Node<>(key, value, p);
// 修复红黑树性质
fixAfterInsertion(p.left);
return;
}
p = p.left;
} else if (cmp < 0) {
if (p.right == null) {
size.increment();
p.right = new Node<>(key, value, p);
// 修复红黑树性质
fixAfterInsertion(p.right);
return;
}
p = p.right;
} else {
p.val = value;
return;
}
}
}
6.4.2. 修复性质
/**
* 插入节点后修复红黑树性质
*
* @param x 当前节点
*/
private void fixAfterInsertion(Node<K, V> x) {
// 1. 情形2:父节点为黑色,无需调整,不进入循环
// 2. 父节点为红色,需要修复,进入循环
while (isRed(x.parent)) {
Node<K, V> p = x.parent;
Node<K, V> g = p.parent;
Node<K, V> u = (p == g.left) ? g.right : g.left;
if (isBlack(u)) {
// 情形4:父节点为红色,叔叔节点为黑色(或叔叔节点不存在)
setColor(g, RED);
if (p == g.left) {
if (x == p.right) {
rotateLeft(p); // 4-3:LR
p = x; // 4-3:LR
}
setColor(p, BLACK); // 4-1:LL
rotateRight(g); // 4-1:LL
} else {
if (x == p.left) {
rotateRight(p); // 4-4:RL
p = x; // 4-4:RL
}
setColor(p, BLACK); // 4-2:RR
rotateLeft(g); // 4-2:RR
}
return;
}
// 情形3:父节点是红色,叔叔节点是红色
setColor(p, BLACK);
setColor(u, BLACK);
if (g == root) return; // 情形1:已经递归到根节点(省略变色过程)
setColor(g, RED);
x = g; // 再次迭代
}
}
6.4.3. 旋转
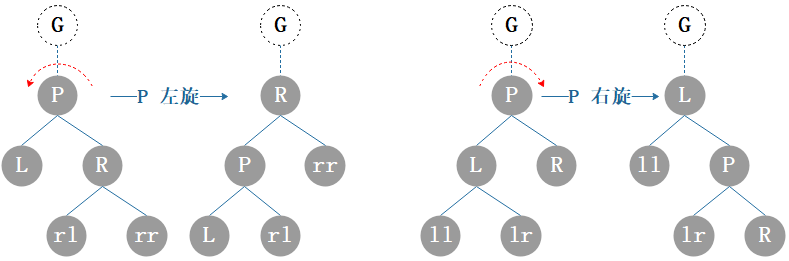
图6.13 旋转
/**
* 左旋
*
* @param p 节点
*/
private void rotateLeft(Node<K, V> p) {
Node<K, V> r = p.right;
p.right = r.left;
if (r.left != null) {
r.left.parent = p;
}
Node<K, V> g = r.parent = p.parent;
if (g == null) {
// 祖父节点为空,r设为根节点
root = r;
} else if (g.left == p) {
g.left = r;
} else {
g.right = r;
}
r.left = p;
p.parent = r;
}
/**
* 右旋
*
* <pre>
* 以 p 节点的左孩子 l 为轴进行旋转:
* p 变成 l 的右孩子;
* lr 变成 p 的左孩子;
* p 的 父节点变成 l;
* l 的父节点变成 p 的父节点 g;
* g g
* / /
* p l
* / \ / \
* l r ll p
* / \ / \
* ll lr lr r
* </pre>
*
* @param p 节点
*/
private void rotateRight(Node<K, V> p) {
Node<K, V> l = p.left;
p.left = l.right;
if (l.right != null) {
l.right.parent = p;
}
Node<K, V> g = l.parent = p.parent;
if (g == null) {
// 祖父节点为空,l设为根节点
root = l;
} else if (g.left == p) {
g.left = l;
} else {
g.right = l;
}
l.right = p;
p.parent = l;
}
7. 删除
大多数算法书对删除操作的介绍都令人难以理解,原因在于省略了演化过程。
所以,除了流程图之外,我会用表格来枚举所有可能的情形并推演各种变化。
7.1. 流程
删除操作相对复杂,因此分为两个流程:主流程描绘整体逻辑;子流程描绘性质修复。
7.1.1. 主流程
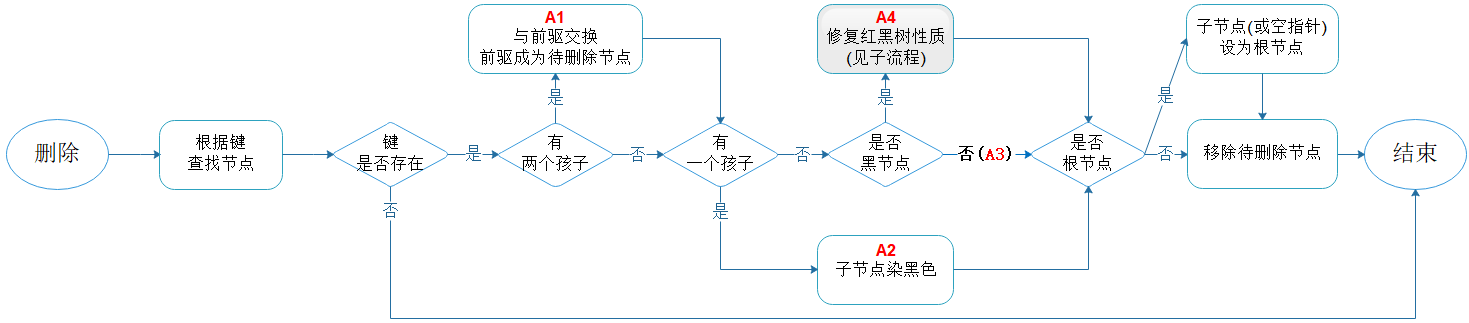
图7.1 删除主流程
流程说明:
- 如果待删除节点有两个子节点,需先与其前驱交换;
- 只有待删除节点为黑色时,才需修复红黑树的性质。
7.1.2. 情形分析
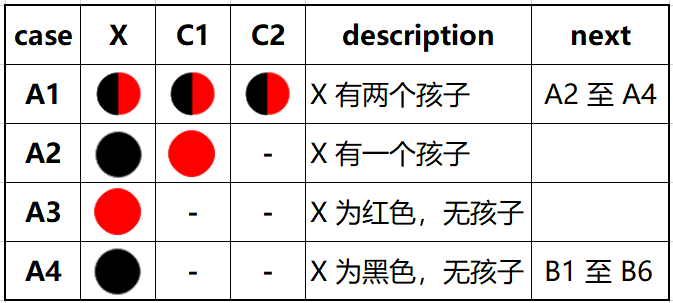
表 7.1 初始情形
A1:待删除节点 X 有两个孩子
操作:待删除节点与前驱节点 (或后继节点) 交换,前驱节点变成了待删除节点。
前驱节点可能没有孩子或仅有一个孩子,这样就将 A1 转化为 A2 至 A4 的情形。
A2:待删除节点 X 有一个孩子
X 必定为黑色,且其唯一子节点必定为红色。
为什么?X 红 C1 红,违反性质4;X 红 C1 黑,X 黑 C1 黑,违反性质5。
操作:删除 X, 性质5 被破坏;C1 红变黑,性质5 被满足,结束。
A3:待删除节点 X 无孩子,且 X 的颜色为红色
操作:删除 X, 仍然满足所有性质,结束。
A4:待删除节点 X 无孩子,且 X 的颜色为黑色
这是最复杂的情况,一共可以枚举出 B 类 6 种情形,详见表7.2。
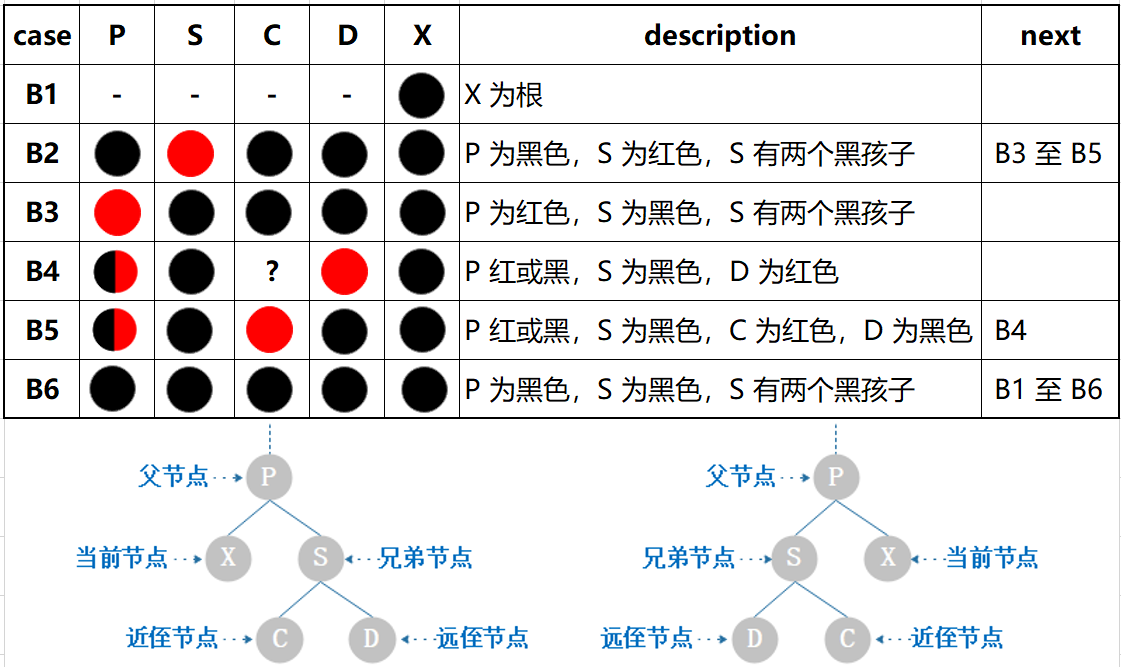
表 7.2 情形枚举
7.1.3. 子流程
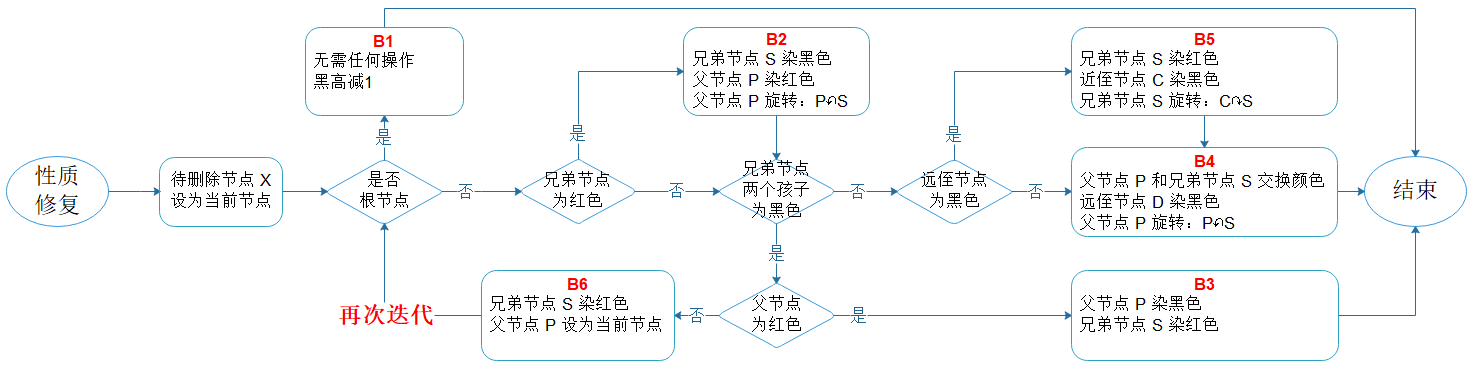
图7.2 删除子流程
流程说明:
- 修复性质需根据父节点、兄弟节点和两个侄子节点的颜色来分别作出不同的处理;
- 只有父节点、兄弟节点、两个侄子节点均为黑色,即情形B6,才会进入再次迭代。
为方便与流程对照,我先将这 6 种情形放在一张图中,如下图所示:
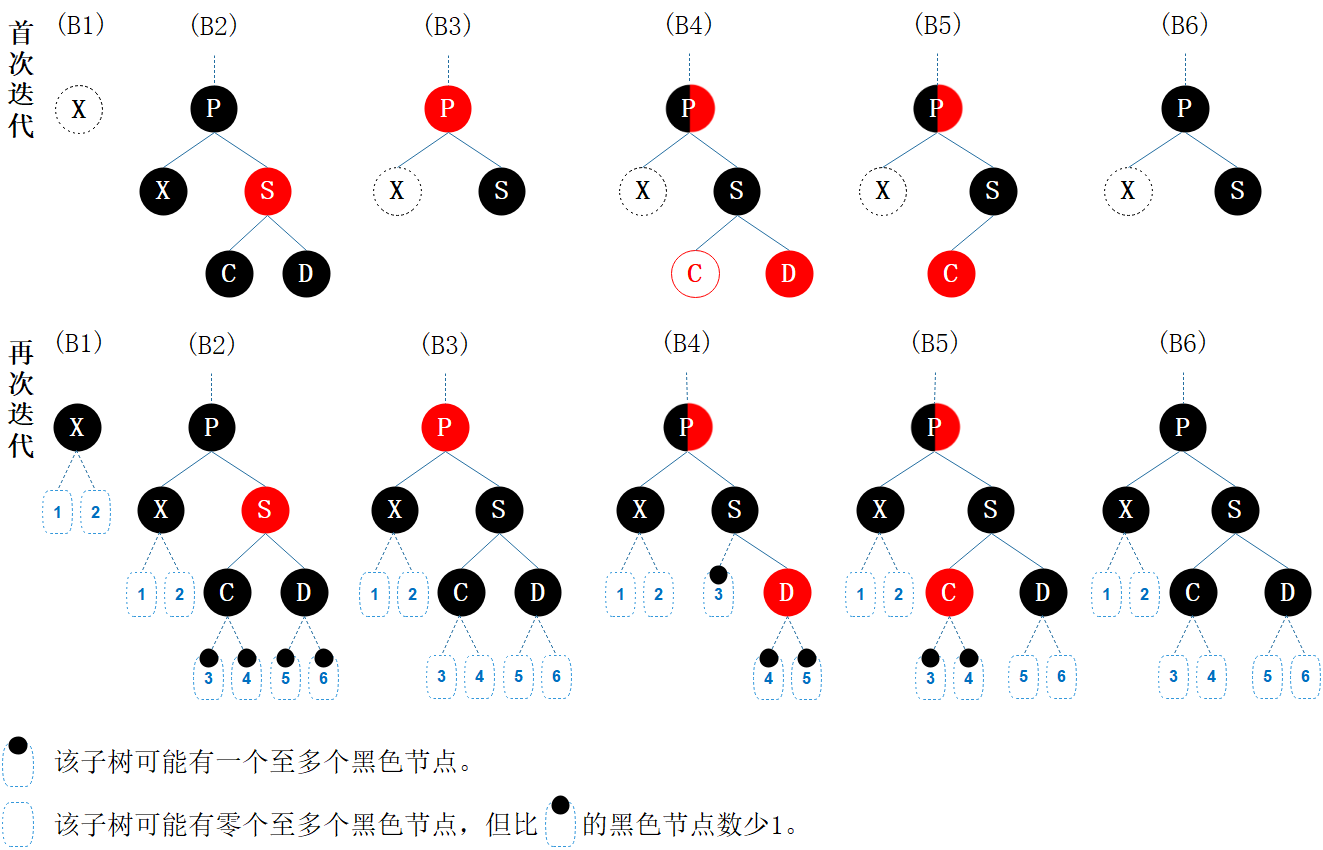
图7.3 删除情形概览
7.2. 删除示例
对于首次迭代,其实是很容易理解的。
比较复杂的是:一种情形会转换为哪一种情形?是如何转换的?什么情况下还需再次迭代?
通过流程图,我们先建立了一个整体概念。接下来,我们就通过操作示例来验证流程逻辑。
7.2.1. 删除示例1
先看一个最简单的例子。
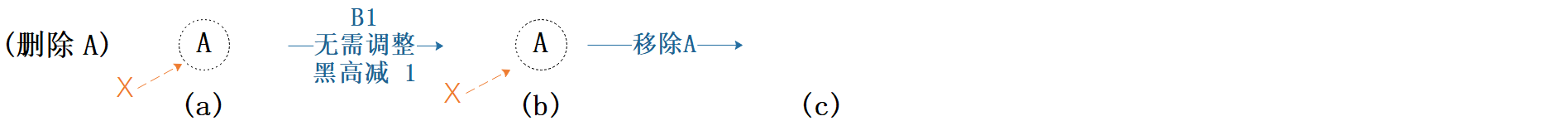
图7.4 删除示例1
(a):当前节点为 A,标记删除 A;A 是树中唯一节点,也就是根节点,符合情形 B1。
(b):首次迭代,无需任何调整,不进入循环体。黑高由 1 变为 0。
(c):正式移除 A,树变成空树。
7.2.1. 删除示例2
再看一个稍复杂的例子。
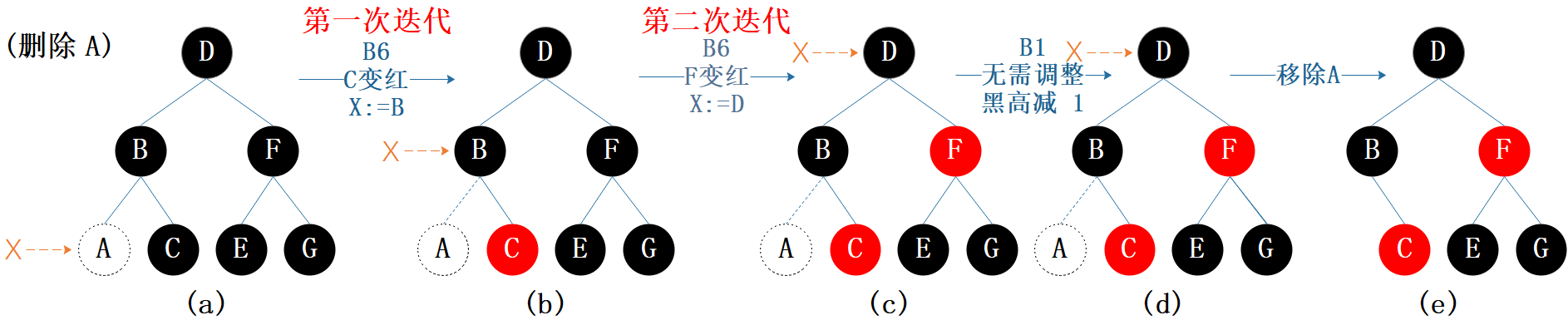
图7.5 删除示例2
(a):
- A 设为当前节点 ,标记删除 A。
- 经过 B 的左孩子(A)的路径上的黑色节点数变为 2,比其它路径少 1,违反性质5。
- A 的父节点 B 和 兄弟节点 C 都为黑色;C 的两个孩子为空,所以也是黑色(根据性质3),符合情形 B6。
(b):
- 兄弟节点 C 染红色。
- 经过 B 的路径上的黑色节点数都变成了 2,比其它路径少 1,违反性质5。
- 当前节点 X 变为其父节点 B,此时 B 是局部平衡的,第一次迭代结束。
- B 的父节点 D 和兄弟节点 F 都为黑色,F 的两个孩子 E 和 G 也是黑色,又再次符合情形B6。
(c):
- 兄弟节点 F 染红色。
- 经过 D 的路径上的黑色节点数都变成了 2。
- 当前节点 X 变为其父节点 D,此时 D 是局部平衡的,第二次迭代结束。
- D 为根, 符合情形B1。
(d):
- 无需调整:由于 D 为根,因此 D 平衡即整棵树平衡。
- 黑高由 3 变为 2。
(e):正式移除 A。
7.2.2. 删除示例3
最后一个更复杂的例子。
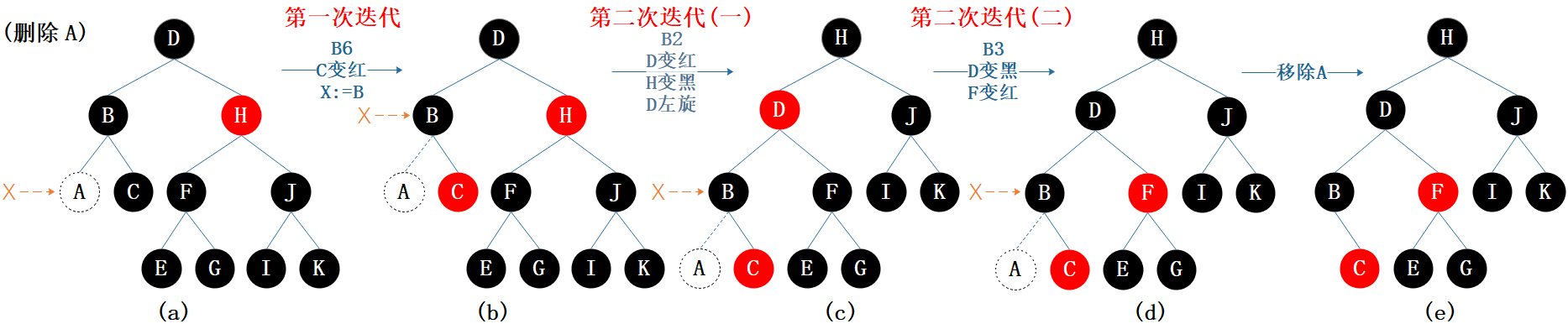
图7.6 删除示例3
(a):
- A 设为当前节点 ,标记删除 A。
- 经过 B 的左孩子(A)的路径上的黑色节点数为 2,比其它路径少 1,违反性质5。
- A 的父节点 B 和 兄弟节点 C 都为黑色,C 的两个孩子为空也是黑色(根据性质3),符合情形 B6。
(b):
- 兄弟节点 C 染红色。
- 经过 B 的路径上的黑色节点数都变成了 2,比其它路径少 1,违反性质5。
- 当前节点变为其父节点 B,此时 B 是局部平衡的,第一次迭代结束。
- B 的兄弟节点 H 为红色,符合情形B2。
(c):
- 父节点 D 染红色,兄弟节点 H 染黑色,父节点 D 左旋;
- 旋转完成后,B 的兄弟节点变成了 F。
- 经过 B 的路径上的黑色节点数还是 2,比其它路径少 1,违反性质5。
- 当前节点还是 B,B 依然是局部平衡的,第二次迭代还未结束。
- B 的父节点 D 为红色, 兄弟节点 F 为黑色,F 的两个孩子 E 和 G 都为黑色,符合情形B3:
(d):
- 父节点 D 染黑色,兄弟节点 F 染红色。
- 经过 B 的路径上的黑色节点数加 1 变为3,与其它路径相等,恢复平衡。
- 第二次迭代结束。
- 黑高不变还是 3。
(e):正式移除 A。
小结
- 所有情形的修复操作都是为了维护性质 5。
- 如果性质修复流程结束于情形 B1 ,那么黑高减 1,其它情形则黑高不变。
- 每一种情形处理完成后,当前节点都是局部平衡的。
- 除非当前节点为根,否则当前节点所在路径上的黑色节点数总是比其它路径少 1。
- 首次迭代时当前节点是待删除节点;再次迭代时变为原当前节点的父节点。
- 如果每次迭代都进入情形 B6,那么迭代过程需到根节点才结束。
7.3. 性质修复
看完示例,我们继续来具体分析每一种情形。
B1:当前节点为根节点

图7.7 删除情形B1
如果是首次迭代就进入 B1,那么 X 是树的唯一节点,移除 X 后就成了空树,黑高由 1 变为 0。
如果是再次迭代才进入 B1,必定是由 B6 演化而来,此时整棵树是平衡的,黑高由 h 变为 h-1。
演化:
首次迭代:B1
再次迭代:B6 —> B1
操作:无需任何调整。
后续:满足所有性质,结束。
B6:父节点、兄弟节点、两个侄子节点都是黑色的
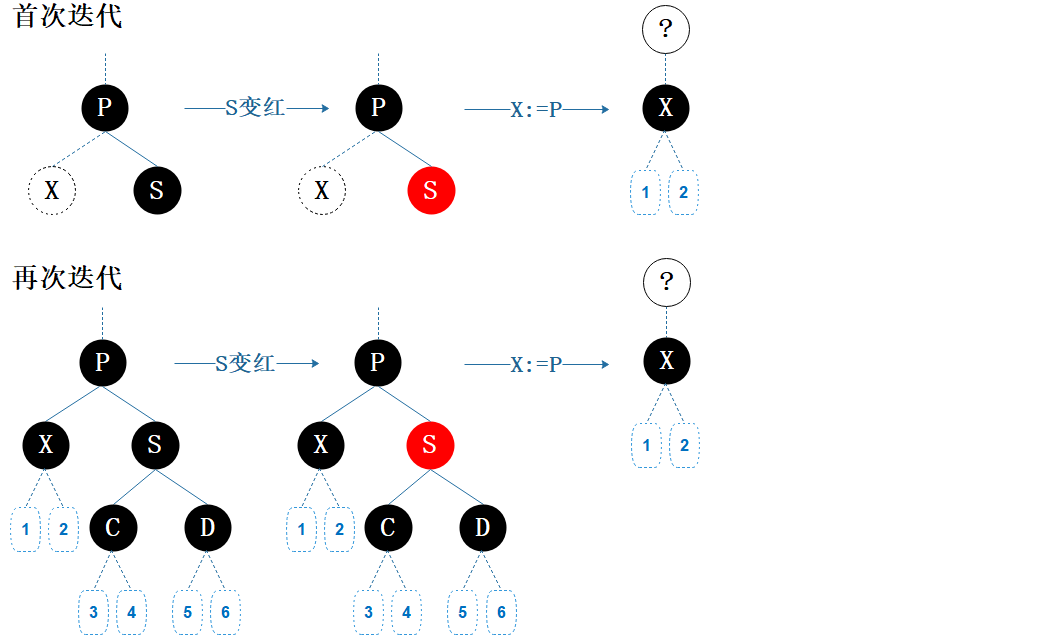
图7.8 删除情形B6
首次迭代时,移除待删除节点 X 后,经过原 X 所在的路径上的黑色节点数会比其它路径少 1。
再次迭代时,上次迭代必定结束于 B6,因此当前节点 X 的路径上的黑色节点数也必定比其它路径少 1。
所有情形都是如此,因此后面的情形不再提示。
演化:
首次迭代:B6
再次迭代:B6 —> B6
操作:
兄弟节点 S 黑变红:父节点 P 达到局部平衡,如果 P 不是根节点,那么 P 所在路径上的黑色节点数比其它路径少 1。
父节点 P 设为当前节点 X:由于新 X 的父节点、兄弟节点、侄子节点都不确定,所以下次迭代时六种情形都有可能。
如果新 X 已经是根节点,那么就会演变成情形 B1。
如果新 X 仍然有父节点,那么就会演变成 B2 至 B6;最坏的情况下,一直都是情形B6,那么需要递归向上处理直到根节点才结束。
后续:仍可能违反性质5,未结束。
B2:兄弟节点为红色
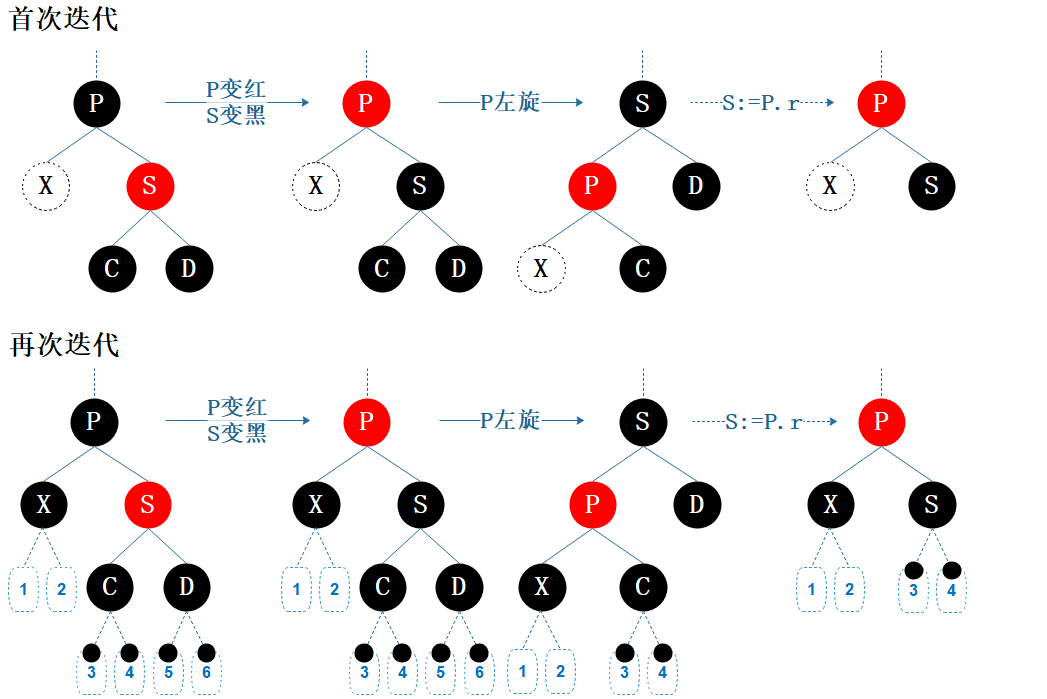
图7.9 删除情形B2
当兄弟节点 S 为红色时,S 的两个孩子 C 和 D 必不为空且一定是黑色,P 也必定为黑色。
演化:
首次迭代:B2
再次迭代:B6 —> B2
操作:兄弟节点 S 染黑色,父节点 P 染红色,父节点 P 左旋。
调整之后,当前节点 X 不变,父节点变为红色,黑色的远侄节点 D变成了其新兄弟节点 ,这可能演化成 B3,B4,B5 这三种情形。
后续:经过 X 的路径上的黑色节点还是少1,仍违反性质5,所以未结束。
B3:父节点为红色,兄弟节点及两个侄子节点都为黑色
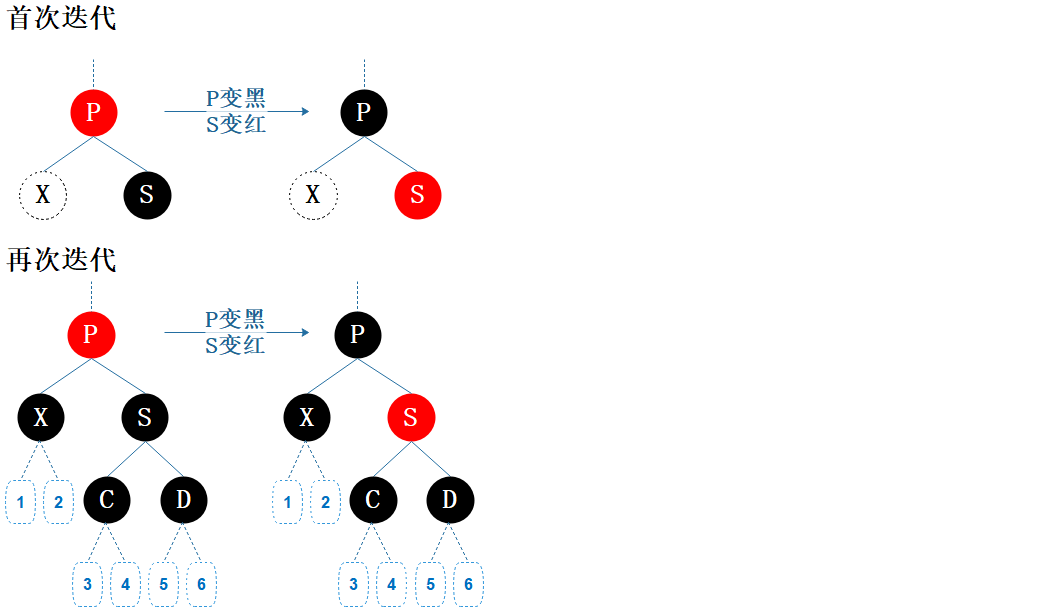
图7.10 删除情形B3
演化:
首次迭代:B3;B2 —> B3
再次迭代:B6 —> B3;B6 —> B2 —> B3
操作: 父节点 P 染黑色:经过 X 的路径上的黑色节点数加 1,与其它路径重新相等;但经过 S 的路径上的黑色节点数也被加 1,比其它路径多 1。
兄弟节点 S 染成红色:经过 S 的路径上的黑色节点数减 1,与其它路径重新相等。
后续:所有性质均满足,结束。
B4:兄弟节点为黑色,远侄节点为红色
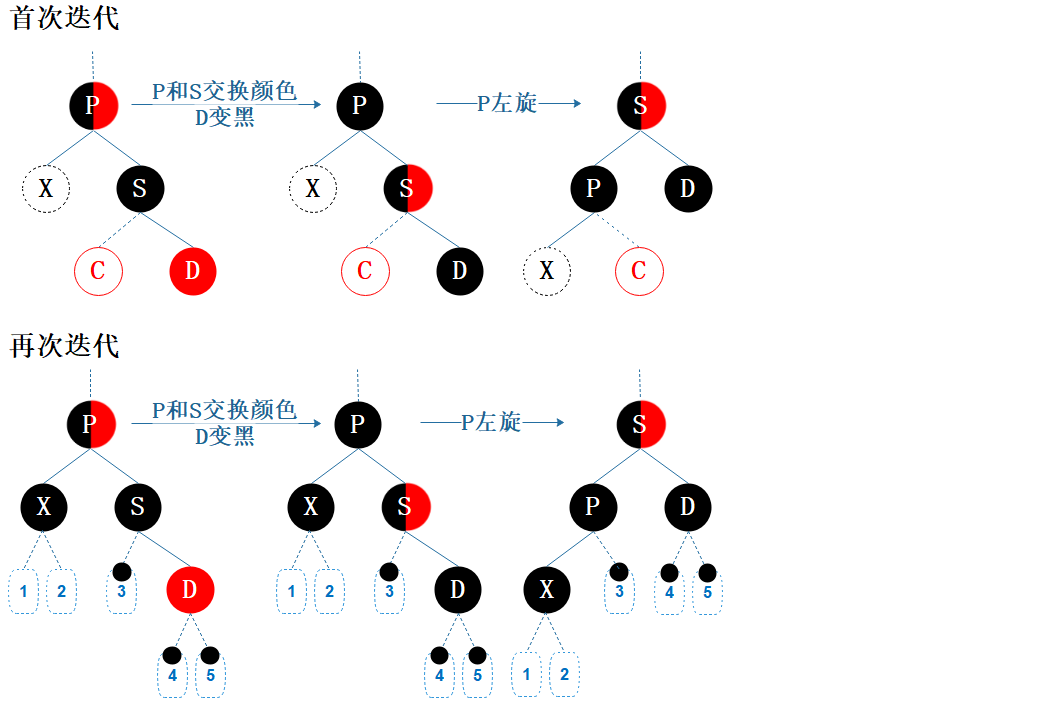
图7.11 删除情形B4
初次迭代时,近侄节点 C 可能是红或空,但肯定不是非空黑节点,否则违反性质 5;
再次迭代时,近侄节点 C 可能是红或黑。
也就是说,情形 B4 不关心 C,只要 S 黑 D 红即可。
演化: 首次迭代:B4;B5 —> B4;B2 —> B4;B2 —> B5 —> B4
再次迭代:B6 —> B4;B6 —> B5 —> B4;B6 —> B2 —> B4;B6 —> B2 —> B5 —> B4
操作:父节点 P 和 兄弟节点 S 交换颜色,远侄节点 D 染黑色,父节点P 左旋。
调整之后,经过 X 的路径上的黑色节点数加 1,与其它路径相等;经过 S 和 D 的路径上的黑色节点数保持不变。
后续:所有性质均满足,结束。
B5:兄弟节点为黑色,近侄节点为红色
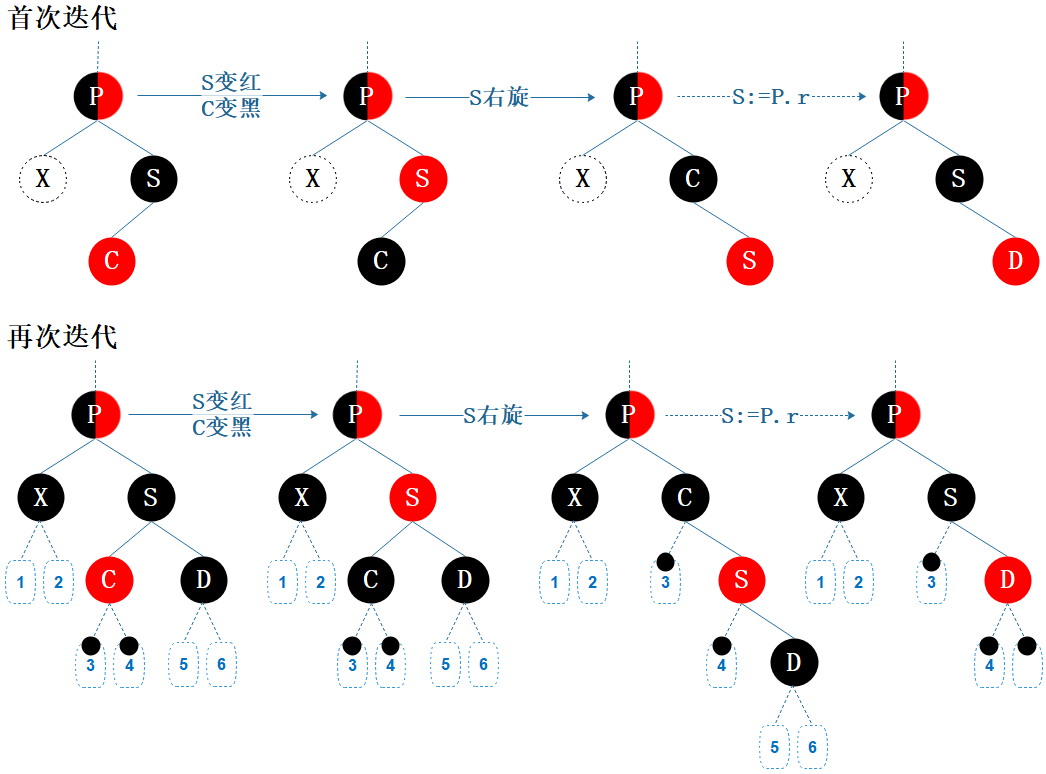
图7.11 删除情形B5
初次迭代时,D 必定为空;再次迭代时,D 为 非空黑节点。D 不可能是红,否则就是情形 B4。
演化:
首次迭代:B5;B2 —> B5
再次迭代:B6 —> B5;B6 —> B2 —> B5
操作:近侄节点 C 染黑色,兄弟节点 S 染红色,兄弟节点 S 右旋。
调整之后,黑 C 成了 X 的兄弟节点 S,红 S 成了 X 的远侄节点 D,这就转换成了情形 B4。
后续:经过 X 的路径上的黑色节点还是少1,仍违反性质 5,所以未结束。
特别说明:
以上图例,X 都是父节点 P 的左孩子。
当 X 为父节点 P 的右孩子时的操作恰好相反,具体处理可看代码及注释。
7.4. 操作等价性
这一小节,我们来探讨红黑树和4 阶 B 树关于删除操作的等价关系。
非叶节点
4 阶 B 树中删除非叶节点中的键,先与前驱(或后继)交换,转换成删除前驱(或后继)的情形。
红黑树中删除有两个孩子的节点,先与前驱(或后继)交换,转换成删除前驱(或后继)的情形 (A1 —> A2 或 A3)。
两者是等价的。
无下溢
4 阶 B 树的 4-节点有3个键,3-节点有2个键,因此删除一个键都不会出现下溢问题。
4-节点删除中间的键:等价于红黑树中待删除节点为黑色,有两个红色子节点 (A1 —> A3)。
4-节点删除两边的键:等价于红黑树中待删除节点为红色 (A3)。
3-节点删除一个键,根据插入顺序不同,也对应这两种情形:
红黑树中待删除节点为红色 (A3);
红黑树中待删除节点为黑色,有一个红色子节点 (A2)。
下溢
4 阶 B 树的 2-节点删除一个键,会出现下溢问题,可以根据兄弟节点的情况,使用不同的方式来处理:
兄弟节点有富余:旋转——等价于红黑树中侄子节点至少有一个为红色(B4,B5)。
兄弟节点无富余:合并——等价于红黑树中侄子节点全部都为黑色(B2,B3,B6)。
4 阶 B 树中,如果当前节点一直是2-节点,而兄弟节点也一直无富余,那么下溢问题会递归向上处理到根节点才结束。
相对应的,红黑树中如果父节点、兄弟节点和侄子节点一直都是黑色 (B6),那么也需要递归向上处理到根节点才结束。
如果出现下溢的节点是根节点,等价于红黑树中当前节点 (待删除节点) 为根节点(B1)。
类比示例
具体看以下示例,我们会看到4阶B树 和红黑树的删除操作是等价的。
看完这些示例,相信也会对为什么要考察父节点、兄弟节点和侄子节点的颜色有更深的理解。
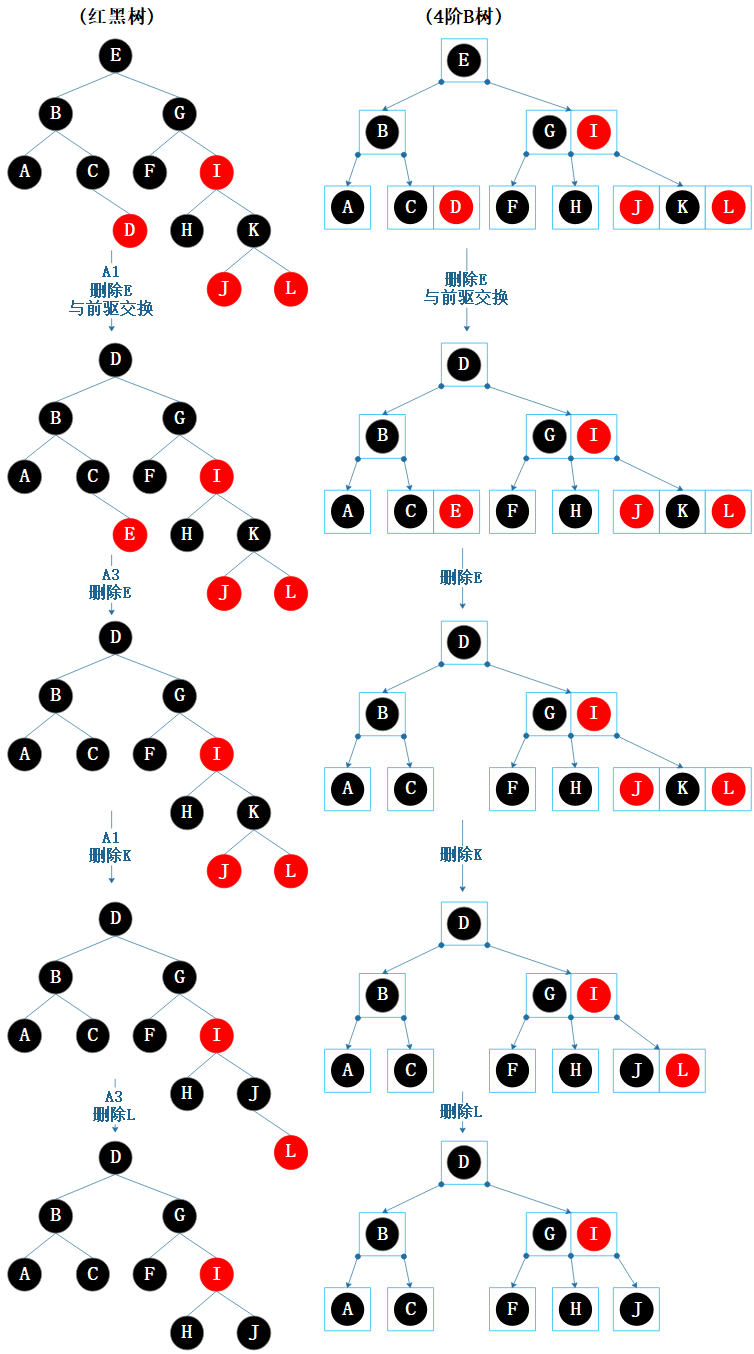
图7.12 删除类比示例1
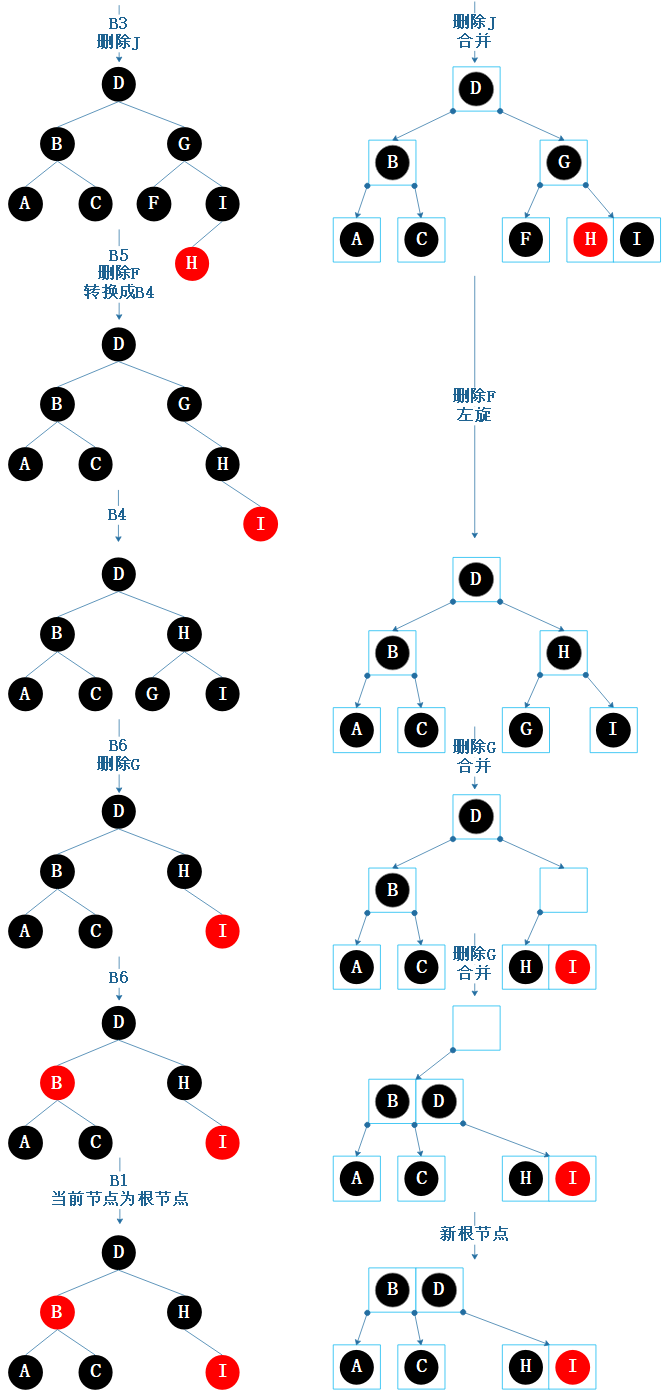
图7.13 删除类比示例2
7.5. 删除情形枚举
有一个很常见的疑问:删除是不是真的只有 6 种情形?我可以肯定地答:是!
通过上一小节的描述其实已经可以推导出只有 6 种情形。
这里我再穷举所有情形,彻底打消这个疑虑,具体看下表。
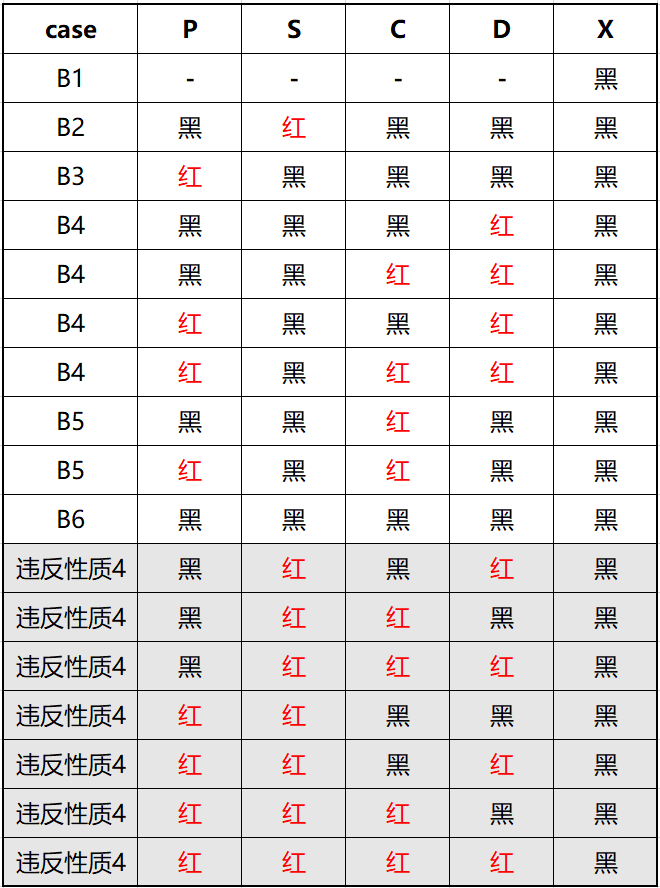
表 7.3 删除情形穷举
7.6. 代码实现
代码参照《算法导论.第3版》7伪码实现并简化了部分逻辑,代码逻辑与流程图一致,可以参照流程图来印证理解。
7.4.1. 删除
@Override
public V remove(K key) {
Node<K, V> x = search(key);
if (x == null) {
return null;
}
V oldVal = x.val;
delete(x);
return oldVal;
}
private void delete(Node<K, V> x) {
size.decrement();
// 是否有两个孩子
if (x.left != null && x.right != null) {
// 情形A1:与前驱交换
x = predecessor(x);
}
// 获取待删除节点的子节点,用以接替待删除节点的位置
Node<K, V> replacement = x.left != null ? x.left : x.right;
if (replacement != null) {
// 情形A2:待删除节点 X 有一个孩子(X 必为黑色,r 必为红色)
// 子节点设为黑色
setColor(replacement, BLACK);
} else {
if (isBlack(x)) {
fixAfterDeletion(x);
}
}
// 移除待删除节点
transplant(x, replacement);
}
/**
* 与前驱交换
*
* @param x 待删除节点
* @return 前驱
*/
private Node<K, V> predecessor(Node<K, V> x) {
Node<K, V> pred = x.left;
while (pred.right != null) {
pred = pred.right;
}
x.key = pred.key;
x.val = pred.val;
return pred;
}
/**
* 移除节点(父节点中指向删除节点的链接变成指向其子节点)
*
* @param x 待删除节点
* @param r 待删除节点的子节点
*/
private void transplant(Node<K, V> x, Node<K, V> r) {
Node<K, V> p = x.parent;
if (p == null) {
// 如果待删除节点为根节点,根变成其子节点
root = r;
return;
}
if (r != null) {
r.parent = p;
}
if (x == p.left) {
p.left = r;
} else {
p.right = r;
}
}
7.4.2. 修复性质
/**
* 删除节点后修复红黑树的性质
*
* @param x 当前节点(待删除节点或其唯一子节点)
*/
private void fixAfterDeletion(Node<K, V> x) {
// 情形 B1:如果x 为根,退出
while (x != root) {
if (x == x.parent.left) {
Node<K, V> s = x.parent.right;
if (s.red == RED) {
// 情形 B2:兄弟节点S 染黑色,父节点P 染红色,父节点P 左旋,未结束
setColor(s, BLACK); // B2
setColor(x.parent, RED); // B2
rotateLeft(x.parent); // B2
s = x.parent.right; // B2
}
if (isBlack(s.left) && isBlack(s.right)) {
// 情形 B3 或 B6:兄弟节点S 染红色,未结束
setColor(s, RED); // B3 或 B6
if (isRed(x.parent)) {
setColor(x.parent, BLACK); // B3
return; // B3
}
x = x.parent; // B6 再次迭代 Δh+1
} else {
if (isBlack(s.right)) {
// 情形 B5:近侄节点C 染黑色,兄弟节点S 染红色,兄弟节点S 右旋,S:=P.r,未结束
setColor(s.left, BLACK); // B5
setColor(s, RED); // B5
rotateRight(s); // B5
s = x.parent.right; // B5
}
// 情形 B4:兄弟节点S 染父节点P 的颜色,父节点P 染黑色,远侄节点D 染黑色,父节点P 左旋,结束
setColor(s, x.parent.red); // B4
setColor(x.parent, BLACK); // B4
setColor(s.right, BLACK); // B4
rotateLeft(x.parent); // B4
return; // B4
}
} else {
Node<K, V> s = x.parent.left;
if (s.red == RED) {
// 情形 B2:兄弟节点S 染黑色,父节点P 染红色,父节点P 右旋,未结束
setColor(s, BLACK); // B2
setColor(x.parent, RED); // B2
rotateRight(x.parent); // B2
s = x.parent.left; // B2
}
if (isBlack(s.left) && isBlack(s.right)) {
// 情形 B3 或 B6:兄弟节点S 染红色,未结束
setColor(s, RED); // B3 或 B6
if (isRed(x.parent)) {
setColor(x.parent, BLACK); // B3
return; // B3
}
x = x.parent; // B6 再次迭代 Δh+1
} else {
if (isBlack(s.left)) {
// 情形 B5:近侄节点C 染黑色,兄弟节点S 染红色,兄弟节点S 左旋,S:=P.l,未结束
setColor(s.right, BLACK); //B5
setColor(s, RED); //B5
rotateLeft(s); //B5
s = x.parent.left; //B5
}
// 情形 B4:兄弟节点S 染父节点P 的颜色,父节点P 染黑色,远侄节点D 染黑色,父节点P 右旋,结束
setColor(s, x.parent.red); // B4
setColor(x.parent, BLACK); // B4
setColor(s.left, BLACK); // B4
rotateRight(x.parent); // B4
return; // B4
}
}
}
}
8. 红黑树的高度
8.1. 最大高度的证明
引理:一棵有 n 个内部节点的红黑树的高度最大为 \( 2log_2(n+1) \) 。
证明:
首先证明以任一节点 x 为根的子树至少包含 \( 2^{bh(x)}-1 \) 个内部节点 【 \( bh(x) \) 是指以 x 为根的子树的黑高 】。
先考虑 x 的黑高等于 0 时的情况:以 x 为根的子树至少包含 \( 2^{bh(x)}-1=2^0-1=0 \) 个内部节点,成立。
再考虑 x 的黑高大于 0 时的情况:
当 x 为黑色时,x 的两个子节点的黑高比 x 的黑高少 1,其每个子节点至少包含 \( 2^{bh(x)-1}-1 \) 个内部节点;
当 x 为红色时,x 的两个子节点的黑高与 x 的黑高相等,其每个子节点至少包含 \( 2^{bh(x)}-1 \) 个内部节点;
两者比较,当 x 为黑色时,内部节点数较少。
因此可得,以 x 为根的子树至少包含 \( (2^{bh(x)-1}-1)+(2^{bh(x)-1}-1)+1=2^{bh(x)}-1 \) 个内部节点,依然成立,由此得证。
现在继续证明引理。
设 \( h \) 为树的高度,根据性质 4,从根到外部节点的任何一条路径上至少有一半的节点为黑色,那么,根的黑高至少为 \( h/2 \) 。于是有:
$$ n \geqslant 2^{h/2}-1 $$1 移到不等式左边,再两边取对数,最后两边乘以 2,可得:
$$ h \leqslant 2log_{2}(n+1) $$证毕。
8.2. 与 AVL 比较
红黑树的平衡条件可以看作是:任意节点的左右子树的高度,相差不超过 2 倍。
AVL 树的平衡条件比红黑树更严格:任意节点的左右子树的高度之差不超过 1 。
理论上红黑树的查询性能会略差,AVL 树的维护性能会略差。
插入
红黑树:2次旋转,或最坏情况下需要递归向上变色直到根节点才结束。
AVL 树:2次旋转,或最坏情况下需要递归向上更新高度直到根节点才结束。
删除
红黑树:3次旋转,或最坏情况下需要递归向上变色直到根节点才结束。
AVL 树:最坏情况下需要递归向上旋转直到根节点才结束。 旋转是结构变化,代价更高。因此对于删除操作,红黑树有较明显的优势。
查询
红黑树的高度:最大为 \( 2log_2(n+1) \);
AVL 树的高度:大约为 \( 1.44log2(n+1) \) ;
因此 AVL 树的查询性能理论上来说会更优。
性能对比
随机生成1000万长度为6~9的字符串,AvlTree 与 RedBlackTree 进行插入、删除和查找的性能对比,测试结果如下(毫秒):
# 测试平台
# CPU:Intel(R) Core(TM) i9-7900X CPU @ 3.30GHz
# RAM:64G DDR4(3000 MHz)
# OS:Win10(21H1)
# JDK:11.0.5
rbt-put: 14877
avl-put: 15984
rbt-get: 13272
avl-get: 13020
rbt-del: 12453
avl-del: 12852
多次运行的测试结果类似。
相比红黑树,AVL 树的插入稍慢查找略快,但两者差别细微,这也符合算法分析的结果。
9. 小结
红黑树算是二叉树中较难理解的结构:一是为什么这样设计,二是删除的情形推理。
为了更直观明了,所以画了很多图,希望能对读者有所有帮助。
参考资料
Bayer, R. “Symmetric binary B-Trees: Data structure and maintenance algorithms”. Acta Informatica 1, 1972. ↩︎ ↩︎ ↩︎
L. J. Guibas and R. Sedgewick. “A dichromatic framework for balanced trees”, 19th Annual Symposium on Foundations of Computer Science, 1978. ↩︎
Andersson, Arne. “Balanced Search Trees Made Simple.” Workshop on Algorithms and Data Structures Springer-Verlag, 1993. ↩︎
OKASAKI, C. “Red-black trees in a functional setting”. Journal of Functional Programming, 1999 ↩︎
Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford. “Introduction to Algorithms (2ed.)”. MIT Press, 2001 ↩︎ ↩︎
Sedgewick, Robert. “Left-leaning Red–Black Trees”, 2008. ↩︎
Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford. “Introduction to Algorithms (3ed.)”. MIT Press, 2009 ↩︎ ↩︎