字典树之旅02：Trie 的标准实现

这篇文章将介绍最简单的 Trie 结构，即 StandardTrie，常被称为标准 Trie，或朴素 Trie。

相关代码：https://github.com/patricklaux/perfect-code

1. 导引

假设有一个关键词集，其中有 6 个单词：bad, bade, bed, ca, cad, dad。

当输入 “b” 时，输出以 “b” 为前缀的所有单词；

输入一段文本，输出文本中存在这六个单词的哪几个，以及单词出现的起止位置……

我们可以建立如下图所示的树形结构。

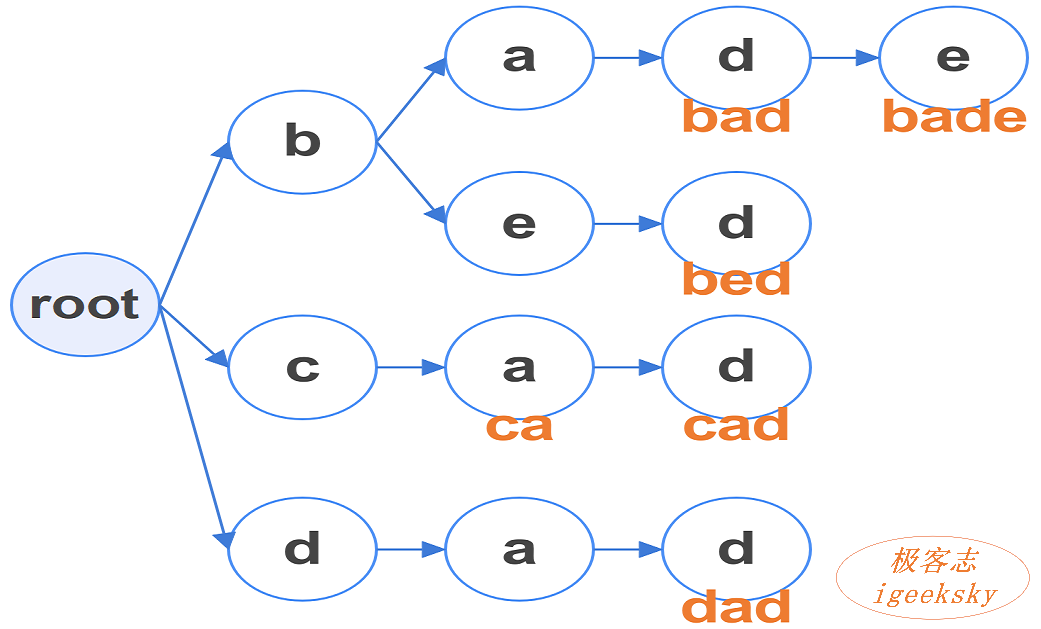
字典树示例

图1：字典树示例

每个字符一个节点，节点之间用边相连；
有特殊标记（有值）则代表一个完整的关键词。

2. 基本性质与操作

通过观察 ”图1：字典树示例“，我们可以发现一些性质和规律。

基本性质

根节点无字符；
兄弟节点的字符互异；
非根节点有且仅有一个字符；
非根节点有且仅有一个父节点；
根节点到其它节点的每条路径代表一个唯一的字符串。

根据以上性质，我们又可以得到一个有意思的推论：6. 兄弟节点都具有同一前缀；

键查找

从根节点沿着序列路径递归查找子节点，最后一个字符对应节点如果有特殊标记，则命中。

譬如要查找 bad，root → b → a → d，命中，返回 bad；譬如查找 cup，root → c → NULL，未命中，返回空。

前缀匹配

先找到前缀节点，然后遍历其子节点。

譬如查找以 b 为前缀的关键词：1. 先找到 b 对应的节点，root → b，找到 b 节点；2. 遍历 b 节点的所有子节点。

3. 代码实现

3.1. 节点定义

package com.igeeksky.perfect.nlp.trie;

private static class StandardNode<V> {
    
    // 因为数组容量R与字符集大小一致，可以省略此字符
    // char c;

    // 值或特殊标记（支持泛型，可以是非字符串）
    V val;

    // 子节点数组，容量为 R
    StandardNode<V>[] table;

    public StandardNode() {
    }

    // R为数组容量
    public StandardNode(int R) {
        this.table = new StandardNode[r];
    }
}

StandardTrie 中所有节点的数组容量相同，其大小与字符表的大小相等。
如使用 UTF-16 字符集，其字符数是 65536，那么数组容量 R 为 65536，则正好可以不重复地映射到数组的位置区间 [0, 65535]。
StandardTrie 中的节点无需显式定义字符，因为可以通过位置隐式转换得到。
譬如，小写字符 ‘a’，转换成 int 值是 97，因此 table[97] 就代表字符 ‘a’。
每个数组的容量均为 R，因此可以将字典树看作是 R 路树。

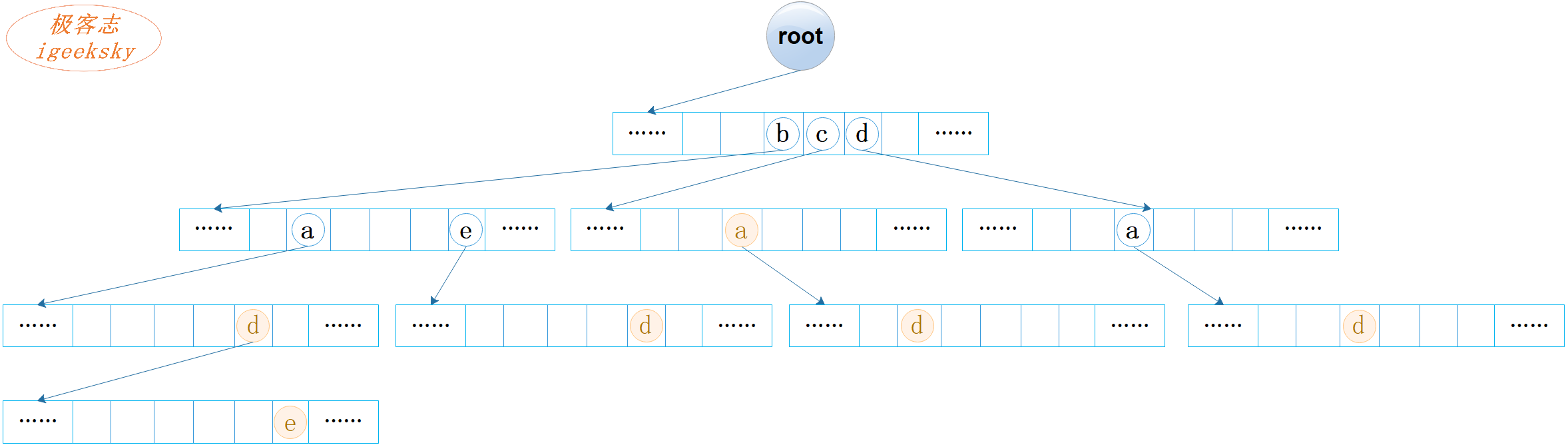
图2：字典树示例（数组）

观察上图，我们会发现有大量的空链接存在，这意味着会有大量的空间被浪费！

这里我们暂且不管空链接问题，先定义接口和实现代码，最后再总结分析其优缺点。

3.2. 接口定义

package com.igeeksky.perfect.api;

/**
 * 字典树接口
 *
 * @author Patrick.Lau
 * @since 1.0.0 2021-11-30
 */
public interface Trie<V> extends BaseMap<String, V> {

    /**
     * 前缀匹配
     * 输入一个字符串，返回树中匹配的最长前缀
     *
     * <pre>
     *     Trie 中已有键：bad, bade, bed, ca, cad, dad
     *     trie.prefixMatch("bades")
     *     返回结果：[bade, bade]
     * </pre>
     */
    Tuple2<String, V> prefixMatch(String word);

    /**
     * 前缀搜索
     * 输入一个字符串，返回树中所有以该字符串为前缀的键值对（可能有多个）
     *
     * <pre>
     *     Trie 中已有键：bad, bade, bed, ca, cad, dad
     *     trie.keysWithPrefix("ca")
     *     返回结果：[[ca, ca], [cad, cad]]
     * </pre>
     */
    List<Tuple2<String, V>> keysWithPrefix(String prefix);

    /**
     * 包含匹配
     * 输入一段文本，判断该文本是否包含树中的键，如果有，则返回键、值及起止位置（可能有多个）
     * 
     * <pre>
     *     Trie 中已有键：bad, bade, bed, ca, cad, dad
     *     trie.matchAll("xxbcaxx")
     *     返回结果：[{"start":3, "end":4, "key":"ca", "value":"ca"}]
     * </pre>
     */
    List<Found<V>> matchAll(String text);
}

Trie 接口继承自 BaseMap，BaseMap 接口还有 put 、get、remove …… 等方法。
Tuple2 是二元组，元素1 为 key，元素2 为 value，元素1 和元素2 均不可变且不能为空。

3.3. 方法实现

3.3.1. Map 方法

public class StandardTrie<V> implements Trie<V> {

    private int size;
    private static final int R = 65536;
    private final BasicNode<V> root = new BasicNode<>(R);

    /**
     * 添加键值对
     *
     * @param key   键
     * @param value 值
     */
    @Override
    @SuppressWarnings("unchecked")
    public void put(String key, V value) {
        int len = key.length();
        if (len == 0) {
            return;
        }
        StandardNode<V> node = root;
        for (int i = 0; i < len; i++) {
            if (node.table == null) {
                // 小优化：只有添加子节点时才创建数组，即叶子节点无数组
                node.table = new StandardNode[R];
            }
            char c = key.charAt(i);
            StandardNode<V> child = node.table[c];
            if (child == null) {
                node.table[c] = (child = new StandardNode<>());
            }
            node = child;
        }
        if(node.val == null){
            ++size;
        }
        node.val = value;
    }

    /**
     * 通过key获取值
     *
     * @param key 键
     * @return 值
     */
    @Override
    public V get(String key) {
        StandardNode<V> node = find(key);
        return (node == null) ? null : node.val;
    }

    /**
     * 移除键值对
     */
    @Override
    public V remove(String key) {
        StandardNode<V> node = find(key);
        if (node == null) {
            return null;
        }
        V oldVal = node.val;
        if (oldVal != null) {
            // 使用惰性删除：仅把关联的值置空，没有真正删除节点
            node.val = null;
            --size;
        }
        return oldVal;
    }

    /**
     * 通过key查找节点
     *
     * @param key 键
     * @return key对应的节点
     */
    private StandardNode<V> find(String key) {
        int len = key.length();
        if (len == 0) {
            return null;
        }
        StandardNode<V> node = root;
        for (int i = 0; i < len; i++) {
            if (node.table == null) {
                return null;
            }
            char c = key.charAt(i);
            node = node.table[c];
            if (node == null) {
                return null;
            }
        }
        return node;
    }
}

代码实现非常非常简单，就是循环查找（添加）子节点而已。

3.3.2. 前缀匹配

输入一个字符串，返回树中匹配的最长前缀。

	/**
     * 前缀匹配：查找 word 的最长前缀
     *
     * @param word 待匹配词（不为空且长度大于0）
     * @return 键值对
     */
	@Override
	public Tuple2<String, V> prefixMatch(String word) {
        int len = word.length();
        if (len == 0) {
            return null;
        }
        StandardNode<V> node = root;
        Tuple2<String, V> tuple2 = null;
        for (int i = 0; i < len; i++) {
            if (node.table == null) {
                return tuple2;
            }
            char c = word.charAt(i);
            node = node.table[c];
            if (node == null) {
                return tuple2;
            }
            if (node.val != null) {
                tuple2 = Tuples.of(word.substring(0, i + 1), node.val);
            }
        }
        return tuple2;
    }

3.3.2. 前缀搜索

输入一个字符串，返回树中所有以该字符串为前缀的键值对。

	/**
     * 查找并返回以 prefix 开头的所有键（及关联的值）
     *
     * @param prefix 前缀（不为空且长度大于0）
     * @return 所有以 prefix 开头的键值对
     */
	@Override
    public List<Tuple2<String, V>> keysWithPrefix(String prefix) {
        List<Tuple2<String, V>> list = new LinkedList<>();
        StandardNode<V> parent = find(prefix);
        traversal(parent, prefix, list);
        return list;
    }

    // 遍历所有后缀节点（深度优先）
    private void traversal(StandardNode<V> parent, String prefix, List<Tuple2<String, V>> list) {
        if (parent != null) {
            if (parent.val != null) {
                list.add(Tuples.of(prefix, parent.val));
            }
            if (parent.table != null) {
                for (int c = 0; c < R; c++) {
                    // 由于数组中可能存在大量空链接，因此遍历时可能会有很多无意义操作
                    String key = prefix + (char) c;
                    StandardNode<V> node = parent.table[c];
                    traversal(node, key, list);
                }
            }
        }
    }

3.3.3. 包含匹配

输入一段文本，判断该文本是否包含树中的键，如果有，则返回键、值及起止位置（可能有多个）。

	/**
     * 查找给定文本段中包含的键
     *
     * @param text 文本段（不为空且长度大于0）
     * @return 结果集（键、值、起止位置）
     */
	@Override
    public List<Found<V>> matchAll(String text) {
        List<Found<V>> list = new LinkedList<>();
        int len = text.length();
        // 每个字符都作为起始字符进行比较
        for (int i = 0; i < len; i++) {
            matchAll(list, text, i, len);
        }
        return list;
    }

    private void matchAll(List<Found<V>> list, String text, int start, int end) {
        StandardNode<V> node = root;
        for (int i = start; i < end; i++) {
            if (node.table == null) {
                return;
            }
            char c = text.charAt(i);
            node = node.table[c];
            if (node == null) {
                return;
            }
            if (node.val != null) {
                list.add(new Found<>(start, i, text.substring(start, i + 1), node.val));
            }
        }
    }

StandardTrie 的相关代码和测试用例都在这里 perfect-code，有兴趣可下载下来慢慢调试。

4. 性能分析

4.1. 时间、空间与动态更新

动态更新：支持，采用指针跳转节点和惰性删除机制，因此动态更新数据的代价极小。
时间性能：非常好，增删查都只跟字符串的长度 m 相关，其时间复杂度最好和最坏的情况都是 O(m)。。
空间性能：非常差，随着树的高度增加，其空间消耗是几何级数增长。如数组容量为 \( R \)，则第一层空间消耗为 \( R \)，第二层可能为 \( R^2 \)，第三层可能为 \( R^3 \)……而且很多数组可能只含 1 个有效节点，却有 \( R-1 \) 个空链接。

4.2. 空间估算

比较准确的空间估算如下：

命题：

一棵标准字典树的链接总数在 R 至 RN(w-1)+R 之间，其中 R 为数组的固定容量，N 为键的数量，w 为键的平均长度。

证明：

由代码实现可知，叶子节点无链接，每个非叶节点都有 R 条链接，每个键都需有一个节点来保存其关联的值。

当 N = 0 时，仅有根节点的数组，链接总数最小，为 R；

当 N > 0 时，如果所有键的首字符均不相同，那么从任意键的第 2 个字符开始都独占一个容量为 R 的数组，链接总数最大，即：RN(w - 1) + R。

注1：根据公式，最大链接数减去节点总数 Nw ，即可得到最大空链接数量公式：RN(w-1) + R - Nw。
注2：这里的证明与《Algorithms. 4th¹》一书的 命题 I 略有不同，是因为这里的代码有小小优化：叶子节点无链接。

例子：

R 为 65536，1000 个键，键的平均长度为10。

最大链接数：65536 × 1000 × (10 - 1) + 65536 = 589889536

最大空链数：589889536 - 1000 × 10 = 589879536

由此可见，极端情况下，空间浪费是非常严重的。

5. 总结

StandardTrie 作为最基础的 Trie 数据结构，实现简单，时间性能很好，支持动态更新。

但由于其空间占用极高，小规模数据集都可能导致 OOM，因此很少直接使用，实际开发中都是用优化后的各种变体。

除了空间占用问题，时间性能其实也有可改进之处，这里不再展开，容我喝几杯咖啡，后续发文慢慢聊。

参考资料

R. Sedgewick and K. Wayne. “Algorithms, fourth edition.” Addison-Wesley(2011):730-753 ↩︎

1. 导引#

2. 基本性质与操作#

基本性质#

键查找#

前缀匹配#

3. 代码实现#

3.1. 节点定义#

3.2. 接口定义#

3.3. 方法实现#

3.3.1. Map 方法#

3.3.2. 前缀匹配#

3.3.2. 前缀搜索#

3.3.3. 包含匹配#

4. 性能分析#

4.1. 时间、空间与动态更新#

4.2. 空间估算#

5. 总结#

参考资料#