字典树之旅04：Patricia Trie(二)

前文实现了 Patricia Trie，但用的是字符比较，而原论文则采用的是二进制位比较。

然后，我们心里可能会有疑问：二进制位比较是如何推广到字符比较的呢？二进制位比较相比于字符比较，又有哪些优点或缺点呢？

相关代码：https://github.com/patricklaux/perfect-code

1. 基数

让我们先从基数说起吧。

1.1. 基数(radix)

基数(radix)，在定位数系(positional numeral system) 中表示不重复编码(digit) 的数量。

譬如在10进制中，有 {0, 1, 2, … ,8, 9} 共 10 个编码，那么基数就是 10；

譬如在16进制中，有 {0, 1, 2, … ,e, f} 共 16 个编码，那么基数就是 16；

…………

如果我们用 EASCII 字符编码来作为集合，那么其基数就是 256；

如果我们用 UTF-16 字符编码来作为集合，那么其基数就是 65536；

…………

如果我们用小写英文字母 {a, b, c, … , y, z} 来作为集合，那么其基数就是26。

也就是说，我们可以根据需要定义一套编码集，而基数就是这套编码集的元素数量。

注：基数(radix) 也可以看作是集合论中的基数(cardinal)，而编码集是有限良序集。

1.2. 基数树(radix tree)

基数概念推广到树中，那么这个基数就是 R 的大小。

我们在前两篇文章的节点定义就有一个 R，用来指定数组容量。类似于如下定义：

class RadixNode{

    // 值
    V val;

    // 子节点数组
    RadixNode<V>[] table;

    // R为数组容量
    public RadixNode(int R) {
        this.table = new RadixNode[R];
    }
}

这棵树会有 R 个分支，又因为编码集是有限良序集，所以可将数组索引映射为唯一编码。

1.3. 基数与二进制

二进制的基数是 2，其编码集合为 {0, 1}；

而数据在计算机中都是用二进制来表示的，

那么，4 进制也可以用二进制编码来表示，其编码集合为 {00, 01, 10, 11}；

然后，8 进制也可以用二进制编码来表示，其编码集合为 {000, 001, … ,110, 111}；

然后，16 进制也可以用二进制编码来表示，其编码集合为 {0000, 0001, … ,1110, 1111}，当然也可以用 { 0, 1, 2, … , e , f }来表示；

…………

最后，我们可以得到一个公式：\( R = 2^r(r>=1) \) ；R 为基数, r 为位数。

当用 4 bit 来表示一个编码时，\( R=2^4=16 \)，那么此时基数就是 16。

…………

7 bit，R 就是 128，正好对应 ASCII 码；

8 bit，R 就是 256，正好对应 EASCII 码；

…………

16 bit，R 就是 65536，正好对应 UTF-16 字符集；

…………

当 R 为 128 或 256 或 65536，我们就回到了字符编码的世界，位与字符的转换已经由编程语言帮我们处理了。

我们还可以选择部分字符来作为编码集，根据需要设计 26 进制，36 进制……等等，正如 16 进制可以用 16 个字符来表示。

既然计算机中数据都是用二进制来表示的，我们当然可以基于位操作来实现 Radix Trie。

1.4. 基数树与二进制

1.4.1. R 为 2

我们先来看看R 为2的情形，此时只有两个编码 {0,1}。我们可以初始化节点：

// 数组大小为 2
RadixNode<V> node = new RadixNode<>(2);

也就是说其构造函数会初始化数组容量为 2：

RadixNode<V>[] table = new RadixNode[2];

我们发现有且仅有两个链接，那么干脆直接将节点定义成二叉树形式：

class BinaryNode{

    // 值
    V val;

    // 左孩子(空 或 0)
    BinaryNode<V> left;
    
    // 右孩子(空 或 1)
    BinaryNode<V> right;

    public BinaryNode() {
    }
}

现在，我们根据这个节点定义来构建一棵树，例如有三个键：“ab”, “ac” 和 “hi”。

首先，将字符串转换成二进制形式（为了避免树太高，这里按 ASCII 编码转换）；

然后，每个 bit 为一个节点，将其保存到树中。如下图所示：

基数树

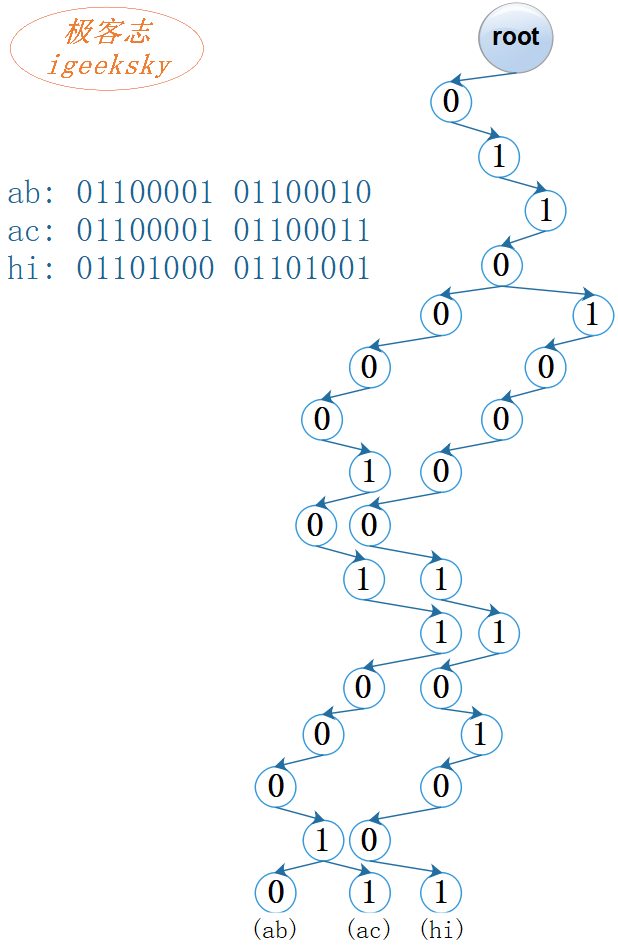
图1：基数树(R=2)

最后，我们得到了一棵高度为16的树。

注：图中标出0和1，仅为帮助理解，节点中无此字段，是隐式定义；节点中也无需保存键。

1.4.2. R 为16

可想而知，仅仅是两个字符的字符串，就需要16次节点查找，效率是非常低的。

那么，我们还可以一个节点保存 4 bit(nibble) ，还是这三个字符串，再画个图：

基数树

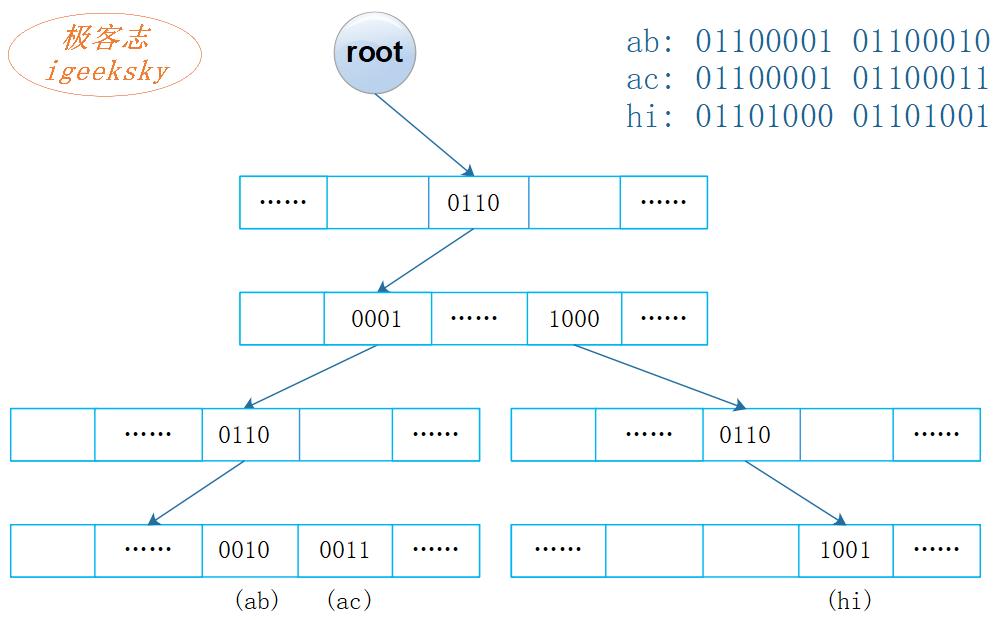
图2：基数树(R=16)

注1：图中标出0110等，仅为帮助理解，节点中无此字段，是隐式含义；节点中也无需保存键。
注2：以太坊的 MPT（Merkle Patricia Tree）就是上图这个结构的复合运用，根节点保存了树的 Hash 值。

这样，树的高度变为 4，但不能再用二叉树了，需要定义一个数组来保存子节点，\( R=2^4=16 \) 。

// 数组大小为 16
RadixNode<V> node = new RadixNode<>(16);

2. 变体

那么，能不能继续用二叉树，但又让树变矮呢？下面来看几个变体。

2.1. 变体一

我们先来定义节点：

class BinaryNode<V>{

    // 键（节点中需保存完整的键）
    // 因为是二进制，键其实可以不局限于字符串，这里为了方便依然设为字符串
    String key;

    // 值
    V val;

    // 左孩子
    BinaryNode<K,V> left;

    // 右孩子
    BinaryNode<K,V> right;
}

具体还是先看张图：

二进制树

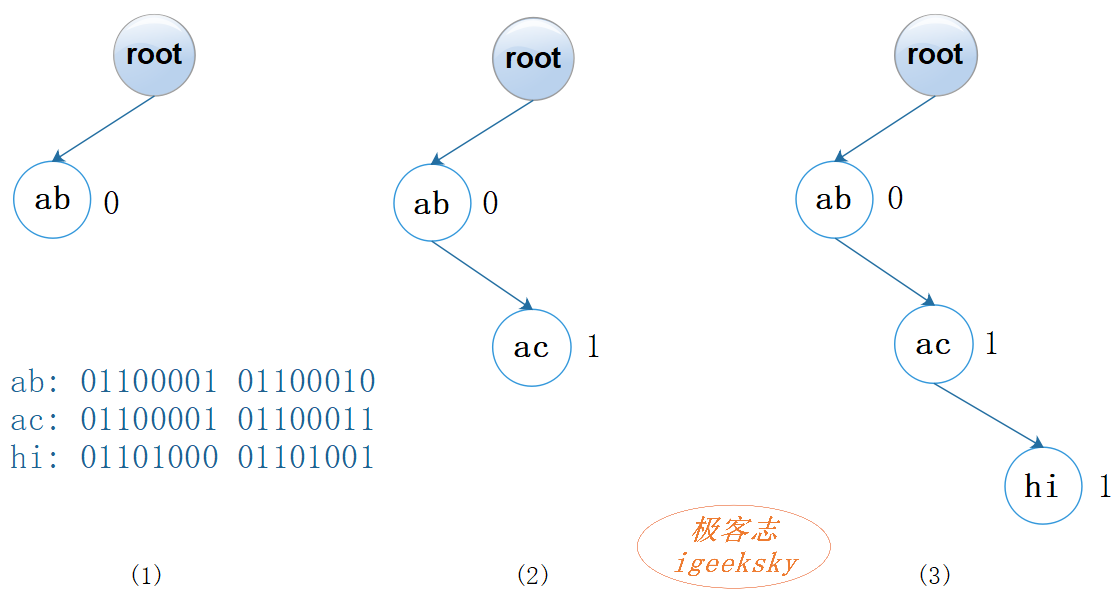
图3：二进制树(变体一)

新增键：

假设键值相同，依次在树中插入 “ab”, “ac” 和 “hi”，过程如下：

插入“ab”：判断 “ab” 的第 0 个 bit，为 0，将其添加为根节点的左孩子；
插入"ac"：判断 “ac” 的第 0 个 bit，为 0，根节点左孩子已存在节点 “ab” 且 “ab” != “ac”；判断第 1 个bit，为 1，将其添加为 “ab” 的右孩子；
插入 “hi”：判断 “hi” 的第 0 个 bit，为 0，根节点左孩子已存在节点 “ab” 且 “ab” != “hi”；判断第 1 个bit，为 1，“ab” 节点已存在右孩子"ac" 且 “ac” != “hi”；判断第 2 个 bit，为 1，将其添加为 “ac” 节点的右孩子。

查找键类似，略。

即是说，树的第 n 层就判断第 n 个bit：如果为0，查找左子树；如果为1，查找右子树。但是，每一层都要判断输入键是否与当前节点的键是否相同。

这个数据结构有点莫名其妙的地方在于：既然每一层都要判断查找键与节点的键是否相同，从计算机硬件层面来说，其实是每一层都要判断两个键的全部 bit 是否完全相同，那这个数据结构按 bit 比较的意义何在？

2.2. 变体二

二进制树

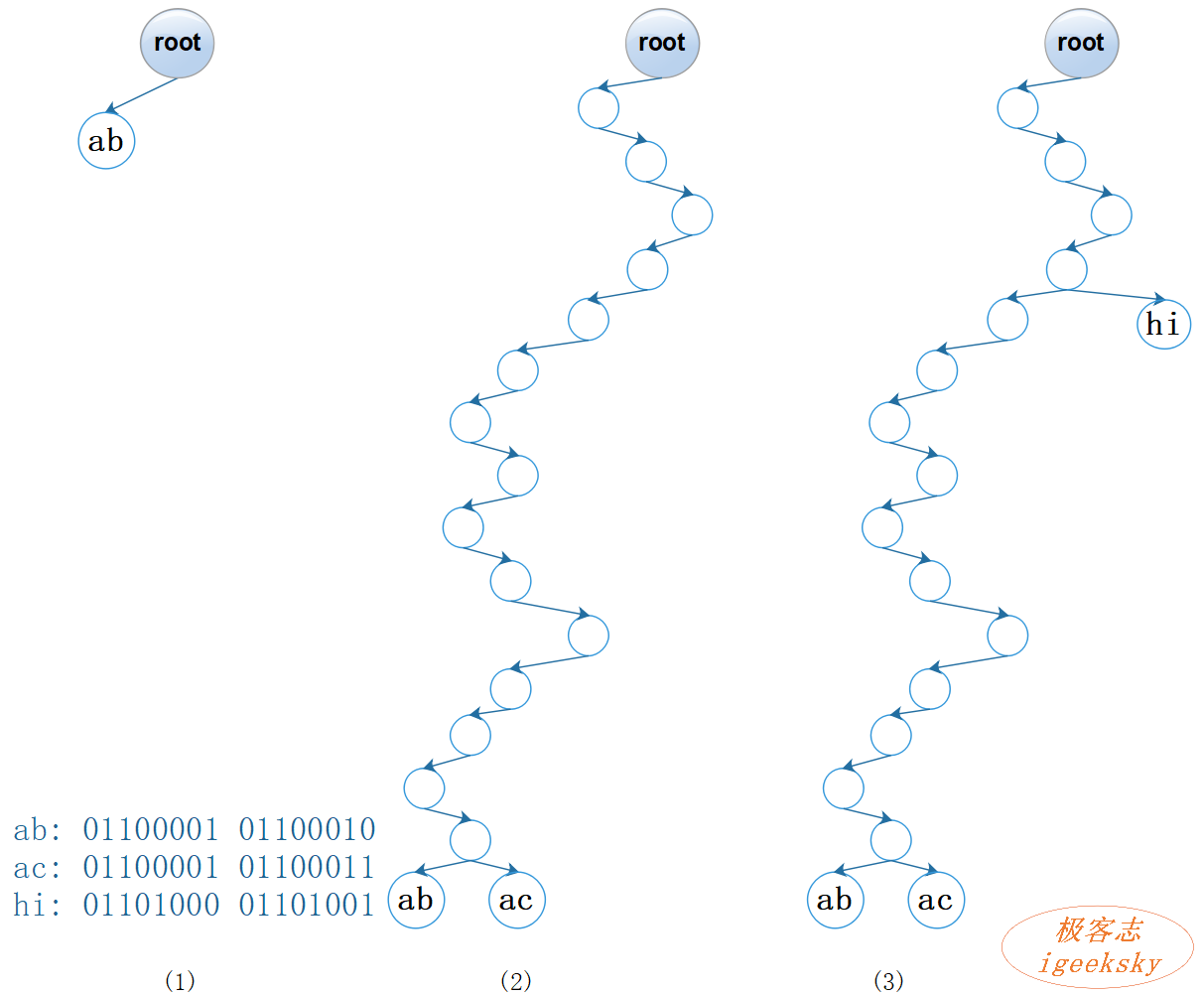
图4：二进制树(变体二)

新增键：

插入“ab”：判断 “ab” 的第 0 个 bit，为 0，将其添加为根节点的左孩子；
插入"ac"：“ab” 和 “ac” 的第 15 个 bit 不同，按 bit 依次添加空节点，最后将第15层空节点的左孩子设为 “ab”，右孩子设为 “ac”。
插入 “hi”：“hi” 的第 4 个 bit 与已存在的节点不同，将 “hi” 设为第4层空节点的右孩子。

查找键（以查找"ab"为例）：

判断 “ab” 的第 0 个 bit，为0，查找左子树；
判断左子树是否为叶子节点，不是叶子节点，判断第 1 个 bit，第 2 个 bit……第15个bit，到达第16层节点；
判断第16层节点是否为叶子节点：是，全键比较。
判断键是否相同：是，返回键值对；否，返回空。

注：
变体二与变体一的不同：变体二仅在叶子节点保存键，因此只需在叶子节点进行全键比较。
变体二与 2.4.1 的不同：变体二消除了单一分支的空节点，叶子节点增加了键字段。

3. PATRICIA

变体二有一个问题：树中有大量的空节点。而 PATRICIA，正是要解决这个问题。

3.1. 节点定义

惯例，我们先定义节点：

private static class PatriciaBinaryNode<V> {
    // 差异位的下标位置
    final int diffIndex;
    // 完整的键
    final String key;
    // 值
    V val;
    // 左孩子
    PatriciaBinaryNode<V> left;
    // 右孩子
    PatriciaBinaryNode<V> right;
    
    // root 的构造方法
    PatriciaBinaryNode() {
        this.diffIndex = 0;
        this.key = String.valueOf('\0');
        this.left = this.right = this;
    }
	// 普通节点构造方法
    PatriciaBinaryNode(int diffIndex, String key, V value) {
        this.diffIndex = diffIndex;
        this.key = key;
        this.val = value;
    }
}

3.2. 查找与新增

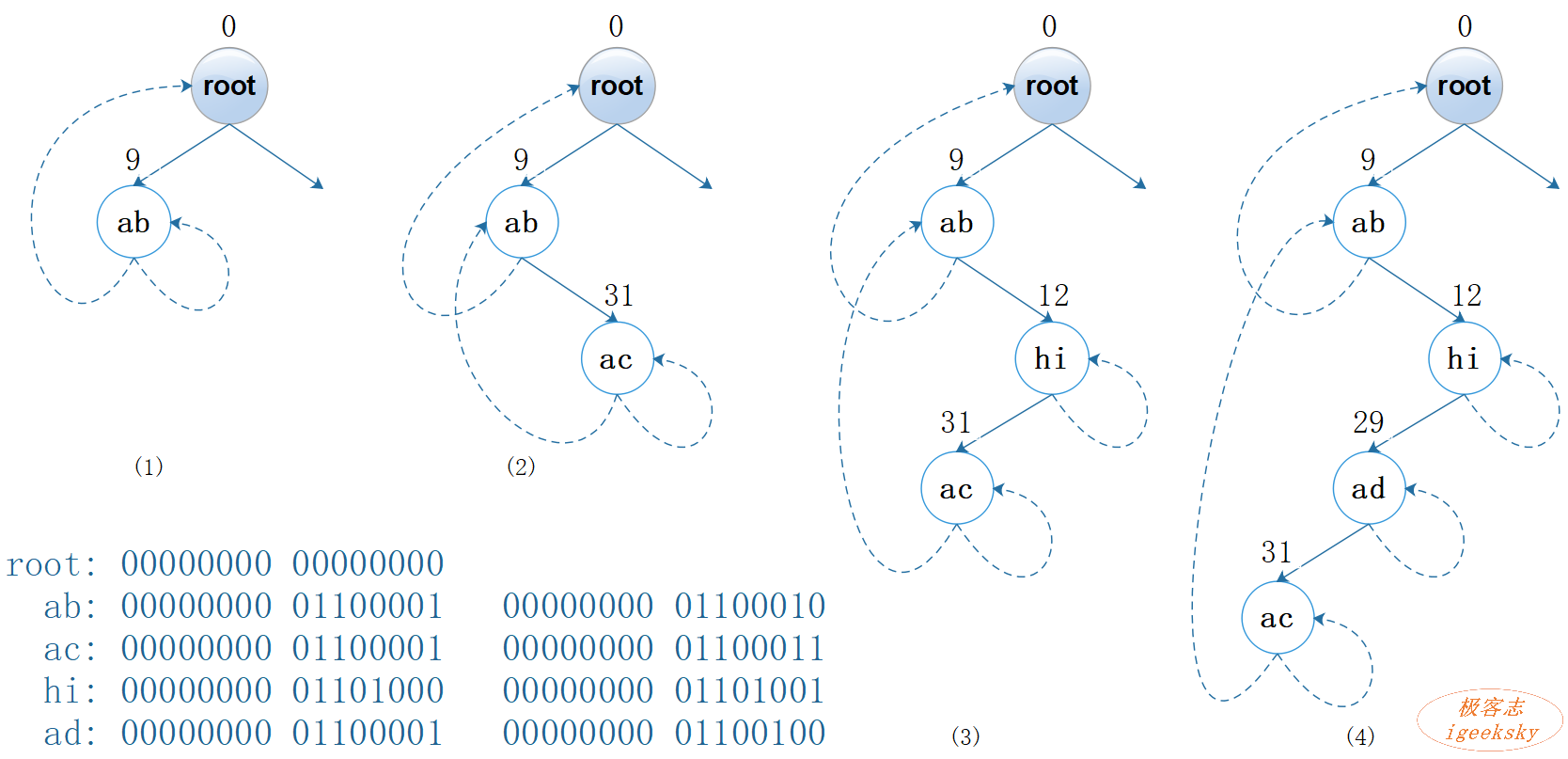
Patricia(二进制)

图5： Patricia(二进制)

图中的虚线为上指链接，即该链接指向自身或祖先节点；
root 节点的字符串为 ‘\0’，差异位的下标 diffIndex 为 0；
为跟代码一致，这里采用 UTF-16 字符集编码进行转换。

3.2.1. 查找键

基本思路：先找到上指链接，然后再判断键是否相同。

从根节点依次向下查找，每次都根据当前所在节点的 diffIndex 获取键的 bit：如果该bit为 0，向左；如果该bit为 1，向右。一旦孩子节点的链接为上指链接，则停止查找 (child.diffIndex <= current.diffIndex)。

这里以查找 “hi” 为例【图5 的 (4)】：

root 节点作为起点，root 节点的 diffIndex 为 0，键"hi" 的第 0 个 bit 为 0，查找左孩子；
左孩子为 “ab” 节点，“ab” 节点的 diffIndex 为 9，键"hi" 的第 9 个 bit 为 1，查找右孩子；
右孩子为 “hi” 节点，“hi” 节点的 diffIndex 为12，键"hi" 的第 12 个bit 为 1，查找右孩子；
“hi” 节点的右孩子为上指链接，该链接指向自身，停止查找。
判断 “hi” 节点的键是否与输入键 “hi” 相同：是，返回值；否，返回空。

3.2.2. 新增键值对

基本思路：先查找，后新增。

这里以新增 “hi” 为例【图5的 (2) → (3)】

首先调用查找方法，找到 “ac” 节点【图5的 (2)】；
比较 “ac” 与 “hi”，找到两者的差异位下标为 12 （用于确定新增节点的位置）；
再次从根节点开始向下查找，当遇到 “ac” 节点的 diffIndex 大于 12，结束查找；
“hi” 的第 9 个 bit为 1，将其添加为 “ab” 节点的右孩子；
“hi” 的第 12 个 bit为 1，“hi” 节点的右孩子指向自身，左孩子指向 “ac” 节点；

最后，将 “hi” 节点新增到 “ab” 节点和 “ac” 节点之间【图5的 (3)】。

3.2.3. 代码实现

public class PatriciaBinaryTrie<V> implements Trie<V> {

    private final IntegerValue size = new IntegerValue();
    private final PatriciaBinaryNode<V> root = new PatriciaBinaryNode<>();

    /**
     * 添加键值对
     *
     * @param key   键
     * @param value 值
     */
    @Override
    public void put(String key, V value) {
        Assert.notNull(value);
        // 1.查找最接近的节点
        PatriciaBinaryNode<V> near = find(key);
        String nearKey = near.key;
        // 2.判断键是否相同，相同则设置并返回，不同则跳到过程3
        if (Objects.equals(key, nearKey)) {
            if (near.val == null) {
                size.increment();
            }
            near.val = value;
            return;
        }
        // 3.找到两个键的差异位
        int diffAt = KeyBits.diffAt(key, nearKey);
        // 4.新增节点
        insert(key, value, diffAt);
    }

    /**
     * 新增节点
     *
     * @param key    键
     * @param value  值
     * @param diffAt 差异位下标
     */
    private void insert(String key, V value, int diffAt) {
        PatriciaBinaryNode<V> path = root, current = (KeyBits.bitAt(key, path.diffIndex) > 0) ? path.right : path.left;
        while (true) {
            /* 
             * 如果 current.diffIndex 大于等于已经比较得到的差异位 diffAt（插入键的范围下界），
             * 或者 current.diffIndex 小于等于 path.diffIndex（遇到上指链接，插入键的范围上界）：
             * 结束查找并新增节点
             */
            if (current.diffIndex >= diffAt || current.diffIndex <= path.diffIndex) {
                PatriciaBinaryNode<V> node = new PatriciaBinaryNode<>(diffAt, key, value);
                // 新增节点的链接指向当前节点
                int bit = KeyBits.bitAt(key, node.diffIndex);
                node.left = bit > 0 ? current : node;
                node.right = bit > 0 ? node : current;
                // 父节点的链接指向新增节点
                bit = KeyBits.bitAt(key, path.diffIndex);
                if (bit > 0) {
                    path.right = node;
                } else {
                    path.left = node;
                }
                size.increment();
                return;
            }
            path = current;
            current = (KeyBits.bitAt(key, current.diffIndex) > 0) ? current.right : current.left;
        }
    }
    
    /**
     * 查找键关联的值
     *
     * @param key 键
     * @return 值
     */
    @Override
    public V get(String key) {
        PatriciaBinaryNode<V> near = find(key);
        return (Objects.equals(key, near.key)) ? near.val : null;
    }

    /**
     * 找到最接近的节点
     *
     * @param key 键
     * @return 与输入的 key 最接近的节点
     */
    private PatriciaBinaryNode<V> find(String key) {
        Assert.hasLength(key);
        PatriciaBinaryNode<V> path = root;
        while (true) {
            PatriciaBinaryNode<V> current = (KeyBits.bitAt(key, path.diffIndex) > 0) ? path.right : path.left;
            if (current.diffIndex <= path.diffIndex) {
                return current;
            }
            path = current;
        }
    }
}

3.3. 分析

无序：

观察图5 ，我们会发现这棵树并不是左小右大，而是无序的。如想要有序，需先预排序再添加。

由于是无序的，因此包含匹配的方法实现会有问题，需额外增加前驱和后继指针，这里就偷个懒😄。

树高：

最坏情况下，树的高度等于最长的键所有位的长度。

如果最长的键有 10 个字符，一个字符按 16 bit 计算，最坏情况下，查找该键需经过 \( 16 × 10 = 160 \) 个节点。

前缀：

任何一个键都不能是另一个键的前缀，但我们可以用一个特殊编码来标记结束（见参考资料¹ P 499）。

如 “a” 和 “ab” 不能同时作为键，因为 “a” 和 “ab” 的前16位相同，而 “a” 没有 17 位，所以无法比较。

我这里是不够长就补一个 ‘\0’（见 com.igeeksky.perfect.nlp.string.KeyBits）。

4. 小结

回到本文开头的问题：

二进制方式和字符方式，两者为什么都是 PatriciaTrie？
Patricia 的核心思想是合并单路分支。无论是字符还是二进制，只要是合并单路分支，就可以认为是 PatriciaTrie（原论文见参考资料²）。
二进制位比较是如何推广到字符比较的？
如果看作是基数树，位比较推广到字符比较，只是基数变化而已。
二进制方式相比于字符方式，有哪些优点或缺点？
二进制方式，空链接少了，但树的高度增加了，时间性能会变差。同时，1 bit 一节点的方式以现在的编程习惯会耗费大量的内存。
综合来看，R 为16 时相对合理，在时间和空间上取得了较好的平衡。

写这篇文章，我恍惚回到了机器语言编程的上古时代，太痛苦了！

最后，让我们忘记二进制位比较吧，因为，后续内容都是基于字符比较的了。

5. 参考资料

Donald E. Knuth. “The Art of Computer Programming. Volume III: Sorting and Searching.” Addison-Wesley(1973):492-512 ↩︎
Morrison, Donald R.. “PATRICIA—Practical Algorithm To Retrieve Information Coded in Alphanumeric.” Journal of the ACM 15 (1968): 514 - 534. ↩︎

1. 基数#

1.1. 基数(radix)#

1.2. 基数树(radix tree)#

1.3. 基数与二进制#

1.4. 基数树与二进制#

1.4.1. R 为 2#

1.4.2. R 为16#

2. 变体#

2.1. 变体一#

2.2. 变体二#

3. PATRICIA#

3.1. 节点定义#

3.2. 查找与新增#

3.2.1. 查找键#

3.2.2. 新增键值对#

3.2.3. 代码实现#

3.3. 分析#

4. 小结#

5. 参考资料#

1. 基数

1.1. 基数(radix)

1.2. 基数树(radix tree)

1.3. 基数与二进制

1.4. 基数树与二进制

1.4.1. R 为 2

1.4.2. R 为16

2. 变体

2.1. 变体一

2.2. 变体二

3. PATRICIA

3.1. 节点定义

3.2. 查找与新增

3.2.1. 查找键

3.2.2. 新增键值对

3.2.3. 代码实现

3.3. 分析

4. 小结

5. 参考资料